
设双曲线C: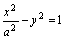 (a>0)与直线l:x+y=1相交于两个不同的点A、B,
(a>0)与直线l:x+y=1相交于两个不同的点A、B,
(1)求双曲线C的离心率e的取值范围;
(Ⅱ)设直线l与y轴的交点为P,且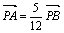 ,求a的值.
,求a的值.
(1)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为了y=x-1.
将y=x-1代入方程y2=4x,并整理得x2-6x+1=0.
设A(x1,y1),B(x2,y2),则有xl+x2=6,x1x2=1.
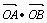 =(x1,y1)·(x2,y2)=x1x2+yly2=2x1x2-(x1 +x2)+1=-3.
=(x1,y1)·(x2,y2)=x1x2+yly2=2x1x2-(x1 +x2)+1=-3.
所以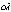 与
与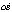 夹角的大小为π-arc cos
夹角的大小为π-arc cos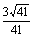 (Ⅱ)由题设
(Ⅱ)由题设 得 (x2-1,y2)=λ(1-x1,-y1),
得 (x2-1,y2)=λ(1-x1,-y1),
即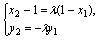 ①
①
②
由②得y22=λ2y21.∵y21=4x1,y22=4x2,∴x2=λ2x1 ③
联立①、③解得x2=λ,依题意有λ>0,∴B(λ,2 )或B (λ,-2 ),又9(1,0),得直线l方程为(λ-1)y= (x-1)或(λ-1)y=2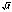 (x-1).当λ∈[4,9]时,l在 y轴上的截距为
(x-1).当λ∈[4,9]时,l在 y轴上的截距为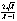 或-
或-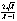
由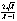 =
=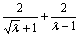 ,可知:
,可知: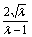 在[4,9]上是递减的,
在[4,9]上是递减的,
∴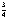 ≤
≤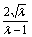 ≤
≤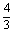 ,-
,-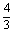 ≤-
≤-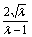 ≤-
≤-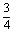
直线l在y轴上截距的变化范围为[-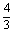 ,-
,-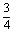 ]∪[
]∪[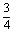 ,
,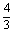 ].
].


科目:高中数学 来源: 题型:
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域 (不含边界)记为W,其左半部分记为W1,右半部分记为W2.

(1)分别用不等式组表示 W1和W2;
(Ⅱ)若区域Ⅳ中的动点p(x,y)到l1,l2的距离之积等于d2,求P点的轨迹C的方程;
(Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于Ml,M2两点,且与l1,l2分别交于M3,M4两点,求证△OM1M2的重心与△OM3M3的重心重合.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,P是抛物线C:y=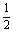 x2上—点,直线l过点P且与抛物线C交于另一点Q.
x2上—点,直线l过点P且与抛物线C交于另一点Q.
(1)若直线l与过点P的切线垂直,求线段PQ中点 M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设椭圆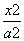 +
+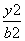 =1(a>b>0)的左、右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左、右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,若直线PF2与圆(x+1)2+(y- )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|=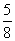 |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com