
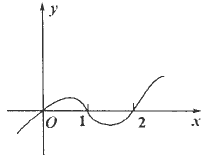
设f(x)=ax3+bx2+cx+d的图象如下图,则b属于
[ ]
A.(-∞,0)
B.(0,1)
C.(1,2)
D.[2,+∞)
|
思路 本题函数图象告诉我们 f(x)在x=0,1,2时的函数值为零或方程ax3+bx2+cx+d=0有解x=0,1,2,可根据此找出解题的突破口.解答 解法一 由图象可得:  
解得 a=-∴ f(x)=-观察图象,知当 x<0时,f(x)<0.而 x,x-1,x-2均小于零,∴-故选 A.(或利用当x>2时,f(x)>0,同样可得b<0).解法二 由图象知: x=0,1,2是方程f(x)=0的三个实根,设 f(x)=ax(x-1)(x-2),当 x>2时,f(x)>0,∴a>0.∵ f(x)=ax(x-1)(x-2)=ax3-3ax2+2ax,又∵ f(x)=ax3+bx2+cx+d,∴b=-3a<0.故选A.评析 虽然我们没有研究过函数 f(x)=ax3+bx2+cx+d(a≠0)的图象和性质,但通过图象提供的信息,运用函数与方程的思想方法还是能够正确地解答该题. |


科目:高中数学 来源:北京市四中2011-2012学年高二下学期期中测试数学理科试题 题型:022
设f(x)=ax3-6ax2+b在区间[-1,2]上的最大值为3,最小值为-29,且a>b,则a=________,b=________.
查看答案和解析>>
科目:高中数学 来源:广东省汕头市金山中学2010届高三期中考试数学理科试题 题型:044
设f(x)=ax3+bx2+4x,其导函数y=![]() (x)的图象经过点(
(x)的图象经过点(![]() ,0),(2,0),如图所示.
,0),(2,0),如图所示.
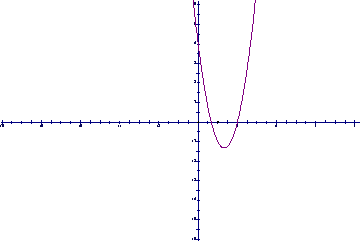
(1)求函数f(x)的解析式和极值;
(2)对x∈[0,3]都有f(x)≥mx2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:贵州省遵义四中2010届高三毕业班第四次月考、文科数学试卷 题型:044
设f(x)=ax3-![]() (a+2)x2+6x-3,x∈R,a是常数,且a>0
(a+2)x2+6x-3,x∈R,a是常数,且a>0
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)若f(x)在x=1时取得极大值,且直线y=-1与函数f(x)的图象有三个交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:甘肃省会宁五中2012届高三10月月考数学理科试题 题型:044
设f(x)=ax3+bx+c为奇函数,其图象在点(1,f(x))处的切线与直线x-6y-7=0垂直,导函数![]() (x)的最小值为-12.
(x)的最小值为-12.
(1)求a,b,c的值;
(2)求函数f(x)的单调递增区间,极大值和极小值,并求函数f(x)在[-1,3]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com