Question

已知数列{a_n}的前n项和为S_n,a₁=1,S_n=a_n+1-3n-1,n∈N^*.

(1)证明数列{a_n+3}是等比数列;

(2)对k∈N*,设f(n)=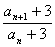求使不等式cos(mπ)［f(2m²)-f(m)］≤0成立的正整数m的取值范围.

Answer 1

解:(1)由S_n=a_n+1-3n-1,则S_n-1=a_n-3(n-1)-1(n≥2),

两式相减并整理,得a_n+1=2a_n+3(n≥2),

即=2(n≥2),又n=1时,a₂=5,=2.

∴数列{a_n+3}是首项为4,公比为2的等比数列.6分

(2)由(1)知a_n+3=4·2^n-1=2ⁿ⁺¹,

S_n=a_n+1-3n-1=2ⁿ⁺²-3n-4,

∴f(n)=

①当m为偶数时,cos(mπ)=1,f(2m²)=2m²+1,f(m)=m+1,

∴原不等式可化为(2m²+1)-(m+1)≤0,

即2m²-m≤0.故不存在符合条件的m.

②当m为奇数时,cos(mπ)=-1,f(2m²)=2m²+1,f(m)=2^m+1-1,

∴原不等式化为2m²+1-2^m+1+1≥0,

即2m²+2≥2^m+1.

当m=1或3时不等式成立;

当m≥5时,2^m+1-1=2(1+1)^m-1=2(+++…++)-1≥2m²+2m+3＞2m²+1.

∴m≥5时原不等式无解.

综合,得当m=1或3时,不等式cos(mπ)［f(2m²)-f(m)］≤0成立.