
已知抛物线C: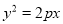
 ,点A、B在抛物线C上.
,点A、B在抛物线C上.

(1)若直线AB过点M(2p,0),且 =4p,求过A,B,O(O为坐标原点)三点的圆的方程;
=4p,求过A,B,O(O为坐标原点)三点的圆的方程;
(2)设直线OA、OB的倾斜角分别为 ,且
,且 ,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
(1)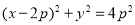 ;(2)过定点
;(2)过定点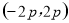
【解析】
试题分析:(1)当直线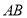 斜率不存在时方程为
斜率不存在时方程为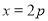 ,与
,与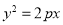 的交点分别为M
的交点分别为M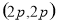 ,N
,N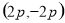 ,弦长
,弦长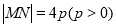 。此时
。此时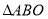 中
中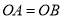 ,
,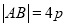 ,
,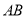 边的中线长为
边的中线长为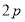 ,所以
,所以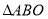 是直角三角形,过
是直角三角形,过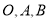 三点的圆的圆心为
三点的圆的圆心为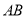 边的中点
边的中点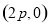 ,半径为
,半径为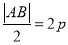 ,则可得此圆的标准方程。(2)设点
,则可得此圆的标准方程。(2)设点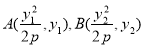 ,为了省去对斜率存在与否的讨论可设直线AB的方程为:
,为了省去对斜率存在与否的讨论可设直线AB的方程为: 。将直线与抛物线方程联立,消去
。将直线与抛物线方程联立,消去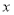 整理为关于
整理为关于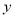 的一元二次方程,可得根与系数的关系。根据
的一元二次方程,可得根与系数的关系。根据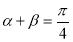 用正切的两角和公式展开可得关于
用正切的两角和公式展开可得关于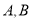 两点坐标
两点坐标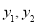 间的关系。根据两关系式可得
间的关系。根据两关系式可得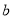 与
与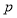 间的关系,故此可判断直线
间的关系,故此可判断直线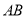 是否过定点。
是否过定点。
试题解析:(1)直线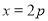 与抛物线
与抛物线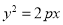 的两个交点坐标分别是:M
的两个交点坐标分别是:M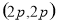 ,N
,N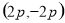 ,弦长
,弦长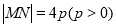 ,故三角形ABO是
,故三角形ABO是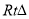 ,所以过A,B,O三点的圆方程是:
,所以过A,B,O三点的圆方程是: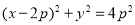
(2)【解析】
设点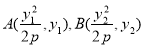 ,直线AB的方程为:
,直线AB的方程为: ,它与抛物线相交,由方程组
,它与抛物线相交,由方程组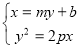 消去x可得
消去x可得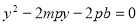 ,故
,故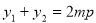 ,
,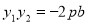 ,
,
这样,tan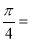
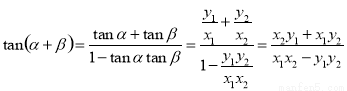
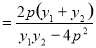
即1=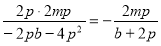 ,所以
,所以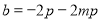 ,所以直线AB的方程可以写成为:
,所以直线AB的方程可以写成为: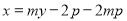 ,即
,即 ,所以直线AB过定点
,所以直线AB过定点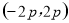 .
.
考点:1圆的标准方程;2抛物线与直线的位置关系问题;3直线过定点问题。


科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:选择题
函数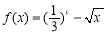 的零点所在区间为( )
的零点所在区间为( )
A.(0,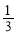 ) B.(
) B.(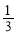 ,
,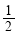 ) C.(
) C.(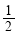 ,1) D.(1,2)
,1) D.(1,2)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
角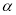 顶点在坐标原点
顶点在坐标原点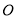 ,始边与
,始边与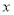 轴的非负半轴重合,
轴的非负半轴重合, ,点
,点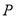 在
在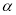 的终边上,点
的终边上,点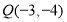 ,则
,则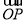 与
与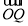 夹角余弦值为( )
夹角余弦值为( )
A.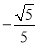 B.
B.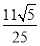 C.
C.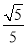 或
或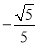 D.
D.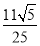 或
或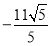
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:填空题
设变量x,y满足约束条件 ,且目标函数
,且目标函数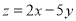 的最小值是
的最小值是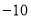 ,则
,则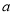 的值是.
的值是.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:选择题
李先生居住在城镇的A处,准备开车到单位B处上班,途中(不绕行)共要经过6个交叉路口,假设每个交叉路口发生堵车事件的概率均为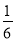 ,则李先生在一次上班途中会遇到堵车次数
,则李先生在一次上班途中会遇到堵车次数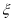 的期望值
的期望值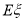 是( )
是( )
A.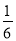 B.1 C.
B.1 C.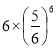 D.
D.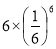
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:填空题
已知函数
 ,若关于
,若关于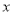 的方程
的方程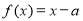 有三个不同的实根,则实数
有三个不同的实根,则实数 的取值范围是.
的取值范围是.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:选择题
正四面体ABCD的棱长为1,其中线段AB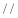 平面
平面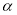 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面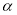 上的射影
上的射影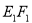 长的范围是( )
长的范围是( )
A.[0,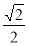 ] B.[
] B.[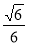 ,
,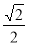 ]
]
C.[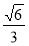 ,
,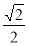 ] D.[
] D.[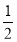 ,
,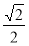 ]
]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)理科数学试卷(解析版) 题型:填空题
已知定义在R上的函数f(x),g(x)满足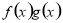 =ax,且f′(x)g(x)+f(x)·g′(x)<0,
=ax,且f′(x)g(x)+f(x)·g′(x)<0,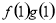 +
+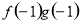 =
=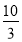 ,若有穷数列{
,若有穷数列{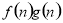 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于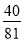 ,则n等于 .
,则n等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com