
分析 ①作出f(x)的图象,根据图象判断;
②将f(x)的图象平移,只需与原图象有3个交点即可.
解答 解:①f(x)=$\left\{\begin{array}{l}{|x-1|,x∈(0,2]}\\{|x-3|,x∈(2,4]}\\{|x-5|,x∈(4,+∞)}\end{array}\right.$,
作出f(x)的函数图象如图所示: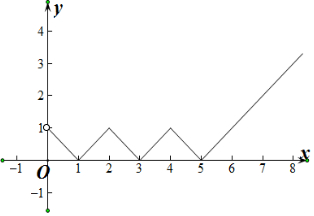
由图象可知当a>1时,f(x)=a只有1解.
②∵关于x的方程f(x+T)=f(x)有且仅有3个不同的实根,
∴将f(x)的图象向左或向右平移|T|个单位后与原图象有3个交点,
∴2<|T|<4,
即-4<T<-2或2<T<4.
故答案为:①(1,+∞),②(-4,-2)∪(2,4).
点评 本题考查方程解与函数图象的关系,函数图象的变换,属于中档题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 26 | C. | 24 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,4) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$)∪(2,+∞) | D. | (0,$\frac{1}{4}$)∪(4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com