
(本题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
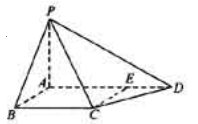
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= 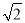 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:2014-2015学年黑龙江省大庆市高三第二次质量检测文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知圆锥曲线 (
(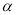 为参数)和定点
为参数)和定点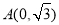 ,
,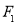 、
、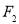 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点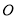 为极点,以
为极点,以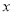 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线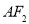 的直角坐标方程;
的直角坐标方程;
(2)经过点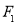 且与直线
且与直线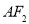 垂直的直线
垂直的直线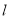 交此圆锥曲线于
交此圆锥曲线于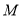 、
、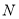 两点,求
两点,求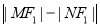 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省等八校高三12月第一次联考文科数学试卷(解析版) 题型:选择题
若幂函数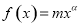 的图象经过点
的图象经过点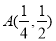 ,则它在点A处的切线方程是( )
,则它在点A处的切线方程是( )
A.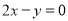 B.
B.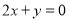
C.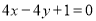 D.
D.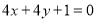
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高三12月月考文科数学试卷(解析版) 题型:选择题
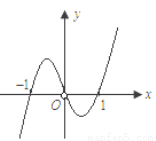
已知函数 的图像如图所示(其中
的图像如图所示(其中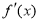 是定义域为R函数
是定义域为R函数 的导函数),则以下说法错误的是( )
的导函数),则以下说法错误的是( )
A.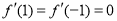
B.当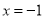 时, 函数
时, 函数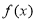 取得极大值[]
取得极大值[]
C.方程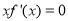 与
与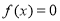 均有三个实数根 []
均有三个实数根 []
D.当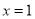 时,函数
时,函数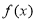 取得极小值
取得极小值
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省保定市高三上学期期末调研考试理科数学试卷(解析版) 题型:填空题
直线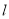 过椭圆
过椭圆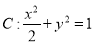 的左焦点
的左焦点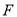 ,且与椭圆
,且与椭圆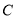 交于
交于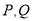 两点,
两点,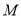 为弦
为弦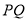 的中点,
的中点,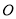 为原点,若
为原点,若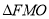 是以线段
是以线段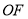 为底边的等腰三角形,则直线
为底边的等腰三角形,则直线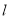 的斜率为
的斜率为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com