
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式,并写出推理过程;
的通项公式,并写出推理过程;
(2)令![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小,并给出你的证明.
的大小,并给出你的证明.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,证明见解析.
,证明见解析.
【解析】试题分析:(Ⅰ)由题意可根据数列通项![]() 与前
与前![]() 项和
项和![]() 之间的关系来进行求解,即当
之间的关系来进行求解,即当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,这时可得到
,这时可得到![]() 与
与![]() 的关系式,根据关系式的特点
的关系式,根据关系式的特点![]() ,可通过构造换元,令
,可通过构造换元,令![]() ,从而得出数列
,从而得出数列![]() 是等差数列,先求出数列
是等差数列,先求出数列![]() 的通项,再求出数列
的通项,再求出数列![]() 的通项;(Ⅱ)根据数列
的通项;(Ⅱ)根据数列![]() 的特点可利用错位相减法求出
的特点可利用错位相减法求出![]() ,接着利用作差法进行比较,根据差式的特点这里可采用数学归纳法进行猜想证明,详见解析.
,接着利用作差法进行比较,根据差式的特点这里可采用数学归纳法进行猜想证明,详见解析.
试题解析:(Ⅰ)在![]() 中,令
中,令![]() ,可得
,可得![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,即当
,即当![]() 时,
时,![]() ,
,
又![]() ,∴数列
,∴数列![]() 是首项和公差均为1的等差数列.
是首项和公差均为1的等差数列.
于是![]() ,∴
,∴![]()
(Ⅱ)由(Ⅰ)得![]() ,
,
所以![]() ,
,
![]()
由①-②,
得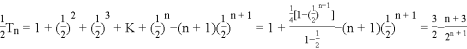
∴![]() ,则
,则![]()
于是只要比较![]() 与
与![]() 的大小即可,
的大小即可,
(1)当![]() 时,
时,![]() ,此时
,此时![]() ,即
,即![]() ,
,
(2)猜想:当![]() 时,
时,![]() ,下面用数学归纳法证明:
,下面用数学归纳法证明:
①当![]() 时,不等式
时,不等式![]() 成立;②假设
成立;②假设![]() 时,不等式成立,即
时,不等式成立,即![]() ;
;
则当![]() 时,
时,![]() ,
,
所以当![]() 时,不等式
时,不等式![]() 成立,
成立,
由①和②可知,当![]() 时,
时,![]() 成立,
成立,
于是,当![]() 时,
时,![]() ,即
,即![]() .
.
另证:要证![]() ,只要证:
,只要证:![]() ,只要证:
,只要证:![]() ,
,
由均值不等式得:![]() ,
,
所以![]() ,于是当
,于是当![]() 时,
时,![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为![]() ,且椭圆C过点P(3,2).
,且椭圆C过点P(3,2).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔参加“全市高中数学竞赛”的选手,某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
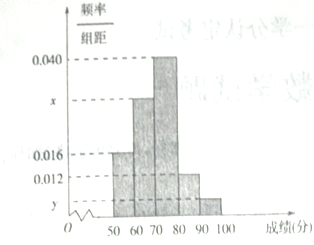
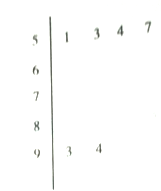
(1)求样本容![]() 和频率分布直方图中
和频率分布直方图中![]() 的值并求出抽取学生的平均分;
的值并求出抽取学生的平均分;
(2)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“全市中数学竞赛”求所抽取的
名学生参加“全市中数学竞赛”求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市有一块半径为40 m的半圆形绿化区域(以O 为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.
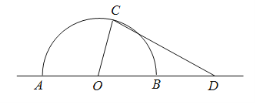
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
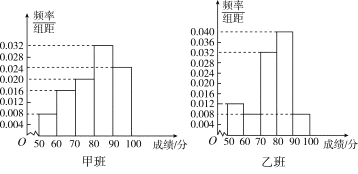
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
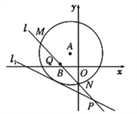
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com