
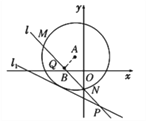
【题目】如图,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
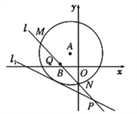
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
【答案】(1) (x+1)2+(y-2)2=20;(2) x=-2或3x-4y+6=0.
【解析】试题分析:(1)利用圆心到切线的距离等于半径求得![]() ;(2)先检验当直线斜率不存在时
;(2)先检验当直线斜率不存在时 ![]() 符合题意;当直线斜率存在是,设其方程为:
符合题意;当直线斜率存在是,设其方程为: ![]() ,再利用点到直线的距离公式和弦长公式,即可求得
,再利用点到直线的距离公式和弦长公式,即可求得![]() ,从而求得另一条直线.
,从而求得另一条直线.
试题解析:(1)设圆A的半径为R.
由于圆A与直线l1:x+2y+7=0相切,
∴R=![]() =2
=2![]() .
.
∴圆A的方程为(x+1)2+(y-2)2=20.
(2)①当直线l与x轴垂直时,易知x=-2符合题意;
②当直线l的斜率存在时,设直线l的方程为y=k(x+2).
即kx-y+2k=0.
连接AQ,则AQ⊥MN.
∵|MN|=2![]() ,∴|AQ|=
,∴|AQ|=![]() =1,
=1,
则由|AQ|=![]() =1,
=1,
得k=![]() ,∴直线l:3x-4y+6=0.
,∴直线l:3x-4y+6=0.
故直线l的方程为x=-2或3x-4y+6=0.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知点A(1,a),圆x2+y2=4.
(1)若过点A的圆的切线只有一条,求a的值及切线方程;
(2)若过点A且在两坐标轴上截距相等的直线被圆截得的弦长为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
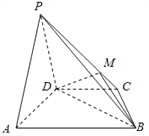
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com