
����Ŀ��ij��ѧ��100���߶��Ŀ����ֳ�ˮƽ��ͬ�ļס���������ƽ�аࡱ��ÿ��50�ˣ�����ʦ����A��B���ֲ�ͬ�Ľ�ѧ��ʽ�ֱ��ڼס�����������н̸�ʵ�飮Ϊ���˽��ѧЧ������ĩ���Ժ���ʦ�Լס��������༶��ѧ���ɼ�����ͳ�Ʒ���������Ƶ�ʷֲ�ֱ��ͼ(����ͼ)���dzɼ�������90����Ϊ���ɼ����㡱��
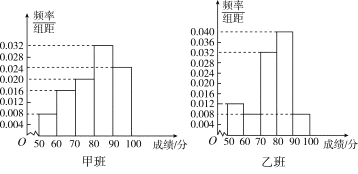
������Ƶ�ʷֲ�ֱ��ͼ��д����2��2��������
�װ�(A��ʽ) | �Ұ�(B��ʽ) | �ܼ� | |
�ɼ����� | |||
�ɼ������� | |||
�ܼ� |
�����ж��ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����ɼ����㡱���ѧ��ʽ�йأ�
����![]() .
.
P(K2��k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
���𰸡���������;�����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����ɼ����㡱���ѧ��ʽ�йأ�
�����������������������Ƶ�ʷֲ�ֱ��ͼ���������ݣ�д�������������������������ݣ�����������۲�ֵ�Ĺ�ʽ�������������е����ݣ��õ��۲�ֵ��ͬ�ٽ�ֵ���бȽϣ��õ����ۣ�
���������������Ƶ�ʷֲ�ֱ��ͼ�ɵã��װ�ɼ����㡢�ɼ�������������ֱ�Ϊ12,38���Ұ�ɼ����㡢�ɼ�������������ֱ�Ϊ4,46.
�װ�(A��ʽ) | �Ұ�(B��ʽ) | �ܼ� | |
�ɼ����� | 12 | 4 | 16 |
�ɼ������� | 38 | 46 | 84 |
�ܼ� | 50 | 50 | 100 |
�������ж������������������ݣ�K2�Ĺ۲�ֵ
![]()
����4.762>3.841�������ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����ɼ����㡱���ѧ��ʽ�йأ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊ��Ȼ�����ĵ�������
Ϊ��Ȼ�����ĵ�������![]()
![]() ��
��![]() ��
��
��1��������![]() ��
��![]() �������߷��̣�
�������߷��̣�
��2�����ۺ���![]() �ļ�Сֵ��
�ļ�Сֵ��
��3�����������![]() ���ܴ���
���ܴ���![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
����������![]() �ĵ������䣻
�ĵ������䣻
��������֤����![]() ��
��
������![]() �ϵ����е㶼����Բ
�ϵ����е㶼����Բ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() .
.
(1)������![]() ��ͨ�ʽ����д���������̣�
��ͨ�ʽ����д���������̣�
(2)��![]() ��
��![]() ���ԱȽ�
���ԱȽ�![]() ��
��![]() �Ĵ�С�����������֤��.
�Ĵ�С�����������֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() �ĵ�������
�ĵ�������
��2�����������![]() ��
��![]() ��
��![]() ����
����![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(1��a)��Բx2��y2��4.
(1)������A��Բ������ֻ��һ������a��ֵ�����߷��̣�
(2)������A�������������Ͻؾ���ȵ�ֱ�߱�Բ�صõ��ҳ�Ϊ![]() ����a��ֵ��
����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Ը�һ�꼶ѧ�����ٲμ���������Ĵ���������ͳ�ƣ������ȡ��![]() ��ѧ����Ϊ�������õ���
��ѧ����Ϊ�������õ���![]() ��ѧ���μ���������Ĵ��������ݴ�����������Ƶ�ʷֲ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�
��ѧ���μ���������Ĵ��������ݴ�����������Ƶ�ʷֲ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�

��1�������![]() ��ֵ��Ƶ�ʷֲ�ֱ��ͼ��
��ֵ��Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ��������Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У��һѧ�����ٲμ����������������λ����
��ֵ��������Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У��һѧ�����ٲμ����������������λ����
��2������÷ֲ�����ķ������������������![]() ��
��![]() �����й���ȡ6�ˣ��ٴ���6����ѡ2�ˣ���2�˷����������
�����й���ȡ6�ˣ��ٴ���6����ѡ2�ˣ���2�˷����������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�ƽ��PAD��ƽ��ABCD��AB��DC����PAD�ǵȱ������Σ���֪AD=4�� ![]() ��AB=2CD=8��
��AB=2CD=8��
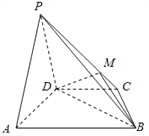
��1����M��PC�ϵ�һ�㣬֤����ƽ��MBD��ƽ��PAD��
��2����M��λ���߶�PCʲôλ��ʱ��PA��ƽ��MBD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]()
��1������![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��2��������![]() �ķ���
�ķ���![]() ������
������![]() �����������ȵĸ�����ʵ��
�����������ȵĸ�����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() ����
����![]() ʱ������
ʱ������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com