
【题目】已知椭圆![]() (a>b>0)经过点
(a>b>0)经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A(0,b),B(a,0),点P是椭圆C上位于第三象限的动点,直线AP、BP分别将x轴、y轴于点M、N,求证:|AN||BM|为定值.
【答案】(1)![]() +y2=1.(2)见解析.
+y2=1.(2)见解析.
【解析】
(1)由题意可得:![]() ,
,![]() ,a2=b2+c2,联立解得:a,b.即可得出椭圆C的方程.
,a2=b2+c2,联立解得:a,b.即可得出椭圆C的方程.
(2)设P(x0,y0),(x0<0,y0<0)A(2,0),B(0,1).![]() .可得直线BP,AP的方程分别为:y=
.可得直线BP,AP的方程分别为:y=![]() x+1,y=
x+1,y=![]() (x-2),可得:M(
(x-2),可得:M(![]() ,0),N(0,
,0),N(0,![]() ).可得|AM||BN|为定值.
).可得|AM||BN|为定值.
解:(1)由题意可得:![]() +
+![]() =1,
=1,![]() =
=![]() ,a2=b2+c2,
,a2=b2+c2,
联立解得:a=2,b=1.
∴椭圆C的方程为:![]() +y2=1.
+y2=1.
(2)证明:设P(x0,y0),(x0<0,y0<0)A(2,0),B(0,1).
![]() +4
+4![]() =4.
=4.
可得直线BP,AP的方程分别为:y=![]() x+1,y=
x+1,y=![]() (x-2),
(x-2),
可得:M(![]() ,0),N(0,
,0),N(0,![]() ).
).
∴|AM|span>|BN|=(2-![]() )(1-
)(1-![]() )=2-
)=2-![]() -
-![]() +
+![]() =
=![]() =4为定值.
=4为定值.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】2018年2月25日第23届冬季奥运会在韩国平昌闭幕,中国以1金6银2铜的成绩结束本次冬奥会的征程.某校体育爱好者协会在高三年级某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从被调查的学生中随机抽取了11人,具体的调查结果如下表:
某班 | 满意 | 不满意 |
男生 | 2 | 3 |
女生 | 4 | 2 |
(Ⅰ)若该班女生人数比男生人数多4人,求该班男生人数和女生人数
(Ⅱ)在该班全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(Ⅲ)若从该班调查对象中随机选取2人进行追踪调查,记选中的2人中对“本届冬奥会中国队表现”满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() (
(![]() ),则称
),则称![]() 是“紧密数列”.
是“紧密数列”.
(1)已知数列![]() 是“紧密数列”,其前5项依次为
是“紧密数列”,其前5项依次为![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若数列![]() 的前
的前![]() 项和为
项和为![]() (
(![]() ),判断
),判断![]() 是否是“紧密数列”,并说明理由;
是否是“紧密数列”,并说明理由;
(3)设![]() 是公比为
是公比为![]() 的等比数列,若
的等比数列,若![]() 与
与![]() 都是“紧密数列”,求
都是“紧密数列”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】魏晋时期数学家刘徽在为《九章算术》作注时,提出利用“牟合方盖”解决球体体积,“牟合方盖”由完全相同的四个曲面构成,相对的两个曲面在同一圆柱的侧面上,正视图和侧视图都是圆,每一个水平截面都是正方形,好似两个扣合(牟合)在一起的方形伞(方盖).二百多年后,南北朝时期数学家祖暅在前人研究的基础上提出了《祖暅原理》:“幂势既同,则积不容异”.意思是:两等高立方体,若在每一等高处的截面积都相等,则两立方体体积相等.如图有一牟合方盖,其正视图与侧视图都是半径为![]() 的圆,正边形
的圆,正边形![]() 是为体现其直观性所作的辅助线,根据祖暅原理,该牟合方盖体积为__________.
是为体现其直观性所作的辅助线,根据祖暅原理,该牟合方盖体积为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,平面
的直径,平面![]() 与半圆
与半圆![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,
, ![]() ,
,![]() 是半圆
是半圆![]() 上不同于
上不同于![]() ,
,![]() 的点,四边形
的点,四边形![]() 是矩形.
是矩形.
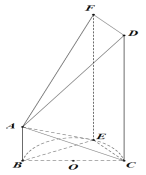
(Ⅰ)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求三棱锥
,求三棱锥![]() 体积的最大值.
体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】α,β是两个不重合的平面,在下列条件中,可判断平面α,β平行的是( )
A. m,n是平面![]() 内两条直线,且
内两条直线,且![]() ,
,![]()
B. ![]() 内不共线的三点到
内不共线的三点到![]() 的距离相等
的距离相等
C. ![]() ,
,![]() 都垂直于平面
都垂直于平面![]()
D. m,n是两条异面直线,![]() ,
,![]() ,且
,且![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com