解:(Ⅰ)f′(x)=3x
2+a,g′(x)=4x,(2分)
由条件知
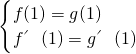
,(4分)
∴
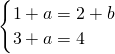
,
∴
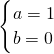
(6分)
(Ⅱ)h(x)=f(x)-mg(x)=x
3+x-2mx
2,
∴h′(x)=3x
2-4mx+1,若h(x)在区间[

,3]上为增函数,
则需h′(x)≥0,即3x
2-4mx+1≥0,∴m≤
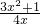
.(9分)
令F(x)=
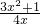
,x∈[

,3],
令F(x)=
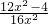
=0,解得x=

,
x,F′(x)及F(x)的变化情况如下:
| x | [ , , ) ) |  | ( ,3] ,3] |
| F'(x) | - | 0 | + |
| F(x) | ↓ | 最小值 | ↑ |
则F(x)在区间[

,3]上的最小值是F(

)=

,
因此,实数m的取值范围是m≤

.(12分)
分析:(Ⅰ)根据题意,把x=1分别代入到f(x)和g(x)中,得到的函数值相等得到关于a与b的方程,分别求出f(x)和g(x)的导函数,把x=1代入导函数中,得到的导函数值相等又得到关于a与b的另一个方程,两方程联立即可求出a与b的值;
(Ⅱ)把f(x)和g(x)的解析式代入确定出h(x)的解析式,求出h(x)导函数,由h(x)在区间上为增函数,得到导函数大于等于0列出不等式,解出m小于等于一个函数,设此函数为F(x),求出F(x)导函数等于0时x的值,根据x的值分区间讨论导函数的正负,从而得到函数的单调性,根据函数的单调性得到函数的最小值,令m小于等于求出的最小值,即可得到m的取值范围.
点评:此题考查了利用导数研究曲线上过某点切线方程的斜率,以及利用导数求闭区间上函数的最值.要求学生掌握求导法则,以及不等式恒成立时满足的条件.

 上是单调增函数,求实数m的取值范围.
上是单调增函数,求实数m的取值范围.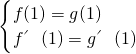 ,(4分)
,(4分)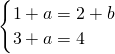 ,
,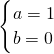 (6分)
(6分) ,3]上为增函数,
,3]上为增函数,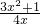 .(9分)
.(9分)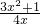 ,x∈[
,x∈[ ,3],
,3],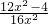 =0,解得x=
=0,解得x= ,
, ,
, )
)
 ,3]
,3]
 ,3]上的最小值是F(
,3]上的最小值是F( )=
)= ,
, .(12分)
.(12分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<