
【题目】已知函数![]() .
.
(1)讨论函数f(x)的极值点的个数;
(2)若f(x)有两个极值点![]() 证明
证明![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)求得函数![]() 的定义域和导函数
的定义域和导函数![]() ,对
,对![]() 分成
分成![]() 三种情况进行分类讨论,判断出
三种情况进行分类讨论,判断出![]() 的极值点个数.
的极值点个数.
(2)由(1)知![]() ,结合韦达定理求得
,结合韦达定理求得![]() 的关系式,由此化简
的关系式,由此化简![]() 的表达式为
的表达式为![]() ,通过构造函数法,结合导数证得
,通过构造函数法,结合导数证得![]() ,由此证得
,由此证得![]() 成立.
成立.
(1)函数![]() 的定义域为
的定义域为![]()
得![]() ,
,
(i)当![]() 时;
时;![]() ,
,
因为![]() 时,
时,![]() 时,
时,![]() ,
,
所以![]() 是函数
是函数![]() 的一个极小值点;
的一个极小值点;
(ii)若![]() 时,
时,
若![]() ,即
,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 是减函数,
是减函数,![]() 无极值点.
无极值点.
若![]() ,即
,即![]() 时,
时,
![]() 有两根
有两根![]() ,
,
![]() 不妨设
不妨设![]()
当![]() 和
和![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 是函数
是函数![]() 的两个极值点,
的两个极值点,
综上所述![]() 时,
时,![]() 仅有一个极值点;
仅有一个极值点;
![]() 时,
时,![]() 无极值点;
无极值点;![]() 时,
时,![]() 有两个极值点.
有两个极值点.
(2)由(1)知,当且仅当![]() 时,
时,![]() 有极小值点
有极小值点![]() 和极大值点
和极大值点![]() ,且
,且![]() 是方程
是方程![]() 的两根,
的两根,
![]() ,则
,则
所以![]()
![]()
![]()
![]()
![]()
设![]() ,则
,则![]() ,又
,又![]() ,即
,即![]() ,
,
所以![]()
所以![]() 是
是![]() 上的单调减函数,
上的单调减函数,![]()
![]() 有两个极值点
有两个极值点![]() ,则
,则![]()


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为常数且
为常数且![]() ,
,![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 和
和![]() 相交于
相交于![]() 、
、![]() 两点,以线段
两点,以线段![]() 为一条边作
为一条边作![]() 的内接矩形
的内接矩形![]() ,当矩形
,当矩形![]() 的面积取最大值时,求
的面积取最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机软件研发公司为改进产品,对软件用户每天在线的时间进行调查,随机抽取40名男性与20名女性对其每天在线的时间进行了调查统计,并绘制了如图所示的条形图,其中每天的在线时间4h以上(包括4h)的用户被称为“资深用户”.
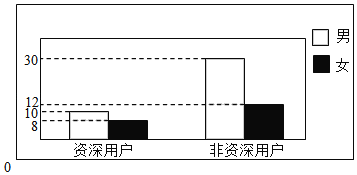
(1)根据上述样本数据,完成下面的2×2列联表,并判定是否有95%的把握认为是否为“资深用户”与性别有关;
“资深用户” | 非“资深用户” | 总计 | |
男性 | |||
女性 | |||
总计 |
(2)用样本估计总体,若从全体用户中随机抽取3人,设这3人中“资深用户”的人数为X,求随机变量X的分布列与数学期望.
附: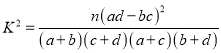 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
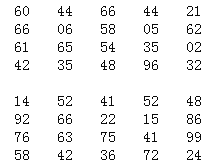
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的准线上一点,F为抛物线的焦点,P为抛物线上的点,且
的准线上一点,F为抛物线的焦点,P为抛物线上的点,且![]() ,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为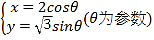 ,在同一平面直角坐标系中,将曲线
,在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换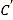 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业现有A.B两套设备生产某种产品,现从A,B两套设备生产的大量产品中各抽取了100件产品作为样本,检测某一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是从A设备抽取的样本频率分布直方图,表1是从B设备抽取的样本频数分布表.
内的产品视为合格品,否则为不合格品.图1是从A设备抽取的样本频率分布直方图,表1是从B设备抽取的样本频数分布表.
图1:A设备生产的样本频率分布直方图
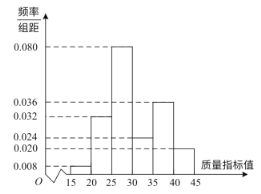
表1:B设备生产的样本频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计A.B设备生产的产品质量指标的平均值;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件利润240元;质量指标值落在
内的定为一等品,每件利润240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件利润180元;其它的合格品定为三等品,每件利润120元.根据图1、表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.企业由于投入资金的限制,需要根据A,B两套设备生产的同一种产品每件获得利润的期望值调整生产规模,请根据以上数据,从经济效益的角度考虑企业应该对哪一套设备加大生产规模?
内的定为二等品,每件利润180元;其它的合格品定为三等品,每件利润120元.根据图1、表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.企业由于投入资金的限制,需要根据A,B两套设备生产的同一种产品每件获得利润的期望值调整生产规模,请根据以上数据,从经济效益的角度考虑企业应该对哪一套设备加大生产规模?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com