
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)是否存在一个正实数![]() ,满足当
,满足当![]() 时,
时,![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() 时,
时,![]() 的增函数区间为
的增函数区间为![]() ,无减函数区间;
,无减函数区间;![]() 时,
时,![]() 的增函数区间为
的增函数区间为![]() ,减函数区间为
,减函数区间为![]() ;
;![]() 时,
时,![]() 的增函数区间为
的增函数区间为![]() ,减函数区间为
,减函数区间为![]() ;(2)存在,
;(2)存在, ![]() .
.
【解析】
(1)根据题意,分析函数定义域,求导,分类讨论参数不同的取值范围时函数单调性,即可求解;
(2)根据题意,![]() ,由(1)知
,由(1)知![]() 的最大值为
的最大值为![]() ,若对任意实数
,若对任意实数![]() ,
,![]() 恒成立,只须使
恒成立,只须使![]() 即可.又因为
即可.又因为![]() ,所以不等式
,所以不等式![]() 等价于:
等价于:![]() ,即:
,即:![]() ,设
,设![]() ,对
,对![]() 求导,分析单调性,讨论
求导,分析单调性,讨论![]() 的范围,判断不等式成立条件.
的范围,判断不等式成立条件.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]()
①若![]() 在
在![]() 上为增函数;
上为增函数;
②若![]() ,∵
,∵![]() ,∴当
,∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数;
上为减函数;
③若![]() ,∵
,∵![]() ,∴当
,∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 为增函数
为增函数
综上可知,![]() 时,
时,![]() 的增函数区间为
的增函数区间为![]() ,无减函数区间;
,无减函数区间;
![]() 时,
时,![]() 的增函数区间为
的增函数区间为![]() ,减函数区间为
,减函数区间为![]() ;
;
![]() 时,
时,![]() 的增函数区间为
的增函数区间为![]() ,减函数区间为
,减函数区间为![]() ;
;
(2)由(1)知,![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
若对任意实数![]() ,
,![]() 恒成立,只须使
恒成立,只须使![]() 即可.
即可.
又因为![]() ,所以不等式
,所以不等式![]() 等价于:
等价于:![]() ,
,
即:![]() ,
,
设![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
所以,![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴当![]() 时,
时,![]() ,不等式
,不等式![]() 不成立,
不成立,
当![]() 时,
时,![]() ,不等式
,不等式![]() 不成立,
不成立,
当![]() 时,
时,![]() ,不等式
,不等式![]() 成立,
成立,
∴存在正实数![]() 且
且![]() 时,满足当
时,满足当![]() 时,
时,![]() 恒成立.
恒成立.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
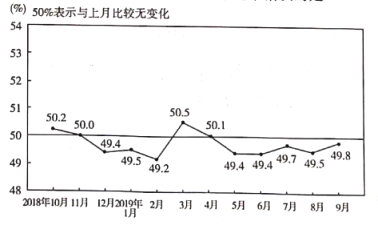
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.回归直线![]() 至少经过其样本数据
至少经过其样本数据![]() 中的一个点
中的一个点
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com