
分析 方法1:求函数的导数,利用导数f′(x)≥0恒成立,利用参数分类法进行求解即可.
方法2:利用函数单调性的定义,利用定义法进行求解即可.
解答 解:函数的导数y′=a-$\frac{2a-1}{{x}^{2}}$,
若函数y=ax-1+$\frac{2a-1}{x}$在[1,2]上是增函数,
则y′≥0恒成立,即a-$\frac{2a-1}{{x}^{2}}$≥0,
即ax2-(2a-1)≥0,
即a(x2-2)+1≥0,
若x=$\sqrt{2}$,则不等式等价为1≥0,不等式成立,
若$\sqrt{2}$<x≤2,则0<x2-2≤2,
则不等式等价为a≥$\frac{-1}{{x}^{2}-2}$,此时,
∵$\frac{-1}{{x}^{2}-2}$≤$\frac{-1}{4-2}=-\frac{1}{2}$,即a$≥-\frac{1}{2}$,
若1≤x<$\sqrt{2}$,则x2-2<0,
则不等式等价为a≤$\frac{-1}{{x}^{2}-2}$,此时$\frac{-1}{1-2}$≤$\frac{-1}{{x}^{2}-2}$,即$\frac{-1}{{x}^{2}-2}$≥1,
则a≤1,
综上$-\frac{1}{2}$≤a≤1.
定义法:
设1≤x1<x2≤2,
则f(x1)-f(x2)=ax1+1+$\frac{2a-1}{{x}_{1}}$-ax2-1-$\frac{2a-1}{{x}_{2}}$=a(x1-x2)+(2a-1)•$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$=(x1-x2)(a-$\frac{2a-1}{{x}_{1}{x}_{2}}$),
∵1≤x1<x2≤2,
∴x1-x2<0,
若函数y=ax-1+$\frac{2a-1}{x}$在[1,2]上是增函数,
则f(x1)<f(x2),即f(x1)-f(x2)<0,
即(x1-x2)(a-$\frac{2a-1}{{x}_{1}{x}_{2}}$)<0,
即a-$\frac{2a-1}{{x}_{1}{x}_{2}}$>0恒成立,
解ax1x2-2a+1>0,
即a(x1x2-2)>-1,
∵1≤x1<x2≤2,
∴1<x1x2<4,
则-1<x1x2-2<2,
若-1<x1x2-2<0,得a<$\frac{-1}{{x}_{1}{x}_{2}-2}$,此时$\frac{-1}{{x}_{1}{x}_{2}-2}$>1,此时a≤1,
若x1x2-2=0,得0>-1成立,
若0<x1x2-2<2,得a>$\frac{-1}{{x}_{1}{x}_{2}-2}$,此时$\frac{-1}{{x}_{1}{x}_{2}-2}$$<-\frac{1}{2}$,此时a≥$-\frac{1}{2}$,
综上$-\frac{1}{2}$≤a≤1.
点评 本题主要考查函数单调性的应用,利用导数法和函数单调性的定义法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
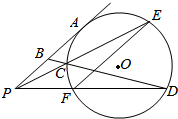 如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.
如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{8}$ | B. | $\frac{9\sqrt{3}}{16}$ | C. | $\frac{9\sqrt{3}}{8}$ | D. | $\frac{9\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com