
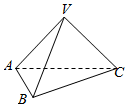
 如图,在三棱锥V-ABC中,VA⊥VC,AB⊥BC,∠VAC=∠ACB=45°,若侧面VAC⊥底面ABC,则其主视图与左视图面积之比为( )
如图,在三棱锥V-ABC中,VA⊥VC,AB⊥BC,∠VAC=∠ACB=45°,若侧面VAC⊥底面ABC,则其主视图与左视图面积之比为( )| A. | 2:1 | B. | 2:$\sqrt{3}$ | C. | $\sqrt{2}$:1 | D. | 1:1 |
分析 由条件可知△VAC,△ABC为等腰直角三角形,故主视图面积为S△VAC,左视图面积为S△BOV.
解答 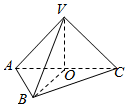 解取AC的中点O,连接OB,OV,
解取AC的中点O,连接OB,OV,
∵VA⊥VC,AB⊥BC,∠VAC=∠ACB=45°,
∴△VAC,△ABC为等腰直角三角形,
∴OV⊥AC,OB⊥AC,
又侧面VAC⊥底面ABC,侧面VAC∩底面ABC=AC,
∴OV⊥平面ABC,OB⊥平面VAC.
设AC=x,OV=h,则OB=$\frac{x}{2}$.
则几何体的主视图面积为S△VAC=$\frac{1}{2}AC•OV$=$\frac{1}{2}xh$.左视图的面积为S△BOV=$\frac{1}{2}OB•OV$=$\frac{1}{4}xh$.
∴$\frac{{S}_{△ACV}}{{S}_{△BOV}}$=2.
故选:A.
点评 本题考查了常见几何体的三视图,属于基础题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 6 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ | $\frac{17π}{6}$ |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
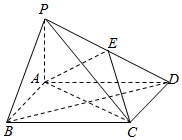 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥面ABCD,E为PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com