Question

8．图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2
（Ⅰ）求证：AC∥平面PBE
（Ⅱ）求平面PBE与平面PAD夹角的余弦值．

Answer 1

分析 （Ⅰ）连接AC，与BD相交于O，取PB的中点H，连接HE，HO，证明四边形OCEH是平行四边形，可得OC∥HE，即可证明AC∥平面PBE
（Ⅱ）建立如图所示的坐标系，求出平面PAD的法向量、平面PBE的法向量，即可求平面PBE与平面PAD夹角的余弦值．

解答 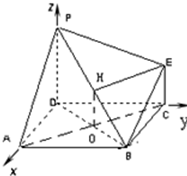（Ⅰ）证明：连接AC，与BD相交于O，取PB的中点H，连接HE，HO，
∵HO是△BDP的中位线，
∴OH∥PD，OH=$\frac{1}{2}$PD，
∵CE∥PD，CE=$\frac{1}{2}$PD，
∴OH∥CE，OH=CE，
∴四边形OCEH是平行四边形，
∴OC∥HE，
∵HE?平面PBE，OC?平面PBE，
∴AC∥平面PBE；
（Ⅱ）解：建立如图所示的坐标系，则D（0，0，0），C（0，2，0），B（2，2，0），P（0，0，2），E（0，2，1），
∴$\overrightarrow{DC}$=（0，2，0）是平面PAD的法向量，
设平面PBE的法向量为$\overrightarrow{n}$=（x，y，z），则
∵$\overrightarrow{BP}$=（-2，-2，2），$\overrightarrow{BE}$=（-2，0，1），
∴$\left\{\begin{array}{l}{-2x-2y+2z=0}\\{-2x+z=0}\end{array}\right.$，
取z=1，则$\overrightarrow{n}$=（$\frac{1}{2}$，$\frac{1}{2}$，1），
∴平面PBE与平面PAD夹角的余弦值|$\frac{1}{2×\frac{\sqrt{6}}{2}}$|=$\frac{\sqrt{6}}{6}$

点评 本题考查线面平行的判定，考查平面PBE与平面PAD夹角的余弦值，正确证明四边形OCEH是平行四边形、求出平面的法向量是关键．