

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 由已知可得,$\overrightarrow{OP}$=$\frac{1}{4m}\overrightarrow{OM}+\frac{1}{4n}\overrightarrow{ON}$,根据三点共线的充要条件,可得$\frac{1}{4m}+\frac{1}{4n}$=1,将m=$\frac{3}{8}$代入,可得n值.
解答 解:∵$\overrightarrow{AB}=2\overrightarrow{AC}$,
故C为线段AB的中点,
故$\overrightarrow{OC}$=$\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}$=2$\overrightarrow{OP}$,
∴$\overrightarrow{OP}$=$\frac{1}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$,
由$\overrightarrow{OM}=m\overrightarrow{OB}$,$\overrightarrow{ON}=n\overrightarrow{OA}$,
∴$\overrightarrow{OB}=\frac{1}{m}\overrightarrow{OM}$,$\overrightarrow{OA}=\frac{1}{n}\overrightarrow{ON}$,
∴$\overrightarrow{OP}$=$\frac{1}{4m}\overrightarrow{OM}+\frac{1}{4n}\overrightarrow{ON}$,
∵M,P,N三点共线,
故$\frac{1}{4m}+\frac{1}{4n}$=1,
当m=$\frac{3}{8}$时,n=$\frac{3}{4}$,
故选:C
点评 本题考查的知识点是平面向量的基本定理及其意义,其中熟练掌握三点共线的充要条件,是解答的关键.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2
图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {0,1} | C. | {0,1,2} | D. | {0,1,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 20 | B. | 5$\sqrt{2}$ | C. | 4($\sqrt{5}$+1) | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (Ⅰ)求抛物线C的方程;
(Ⅰ)求抛物线C的方程;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
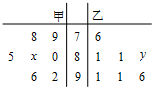 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 7 | C. | 9 | D. | 168 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com