
 (0)
(0)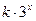 )+f(3
)+f(3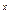 -9
-9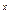 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围. ,则有
,则有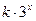 )<-f(3
)<-f(3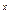 -9
-9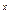 -2)=f(-3
-2)=f(-3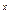 +9
+9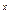 +2),
+2), 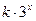 <-3
<-3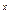 +9
+9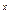 +2,
+2,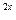 -(1+k)
-(1+k)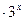
 +2>0对任意x∈R成立. …… …………………8分
+2>0对任意x∈R成立. …… …………………8分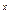 >0,问题等价于t
>0,问题等价于t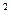 -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.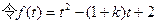 ,其对称轴为
,其对称轴为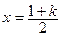
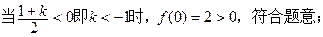 ………………10
………………10 分
分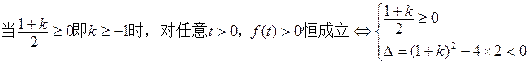 解得:
解得: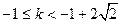
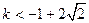 时,f(
时,f(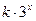 )+f(3
)+f(3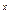 -9
-9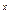 -2)<0对任意x∈R恒成立.
-2)<0对任意x∈R恒成立.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com