
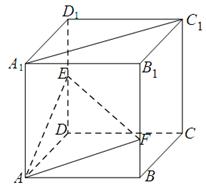
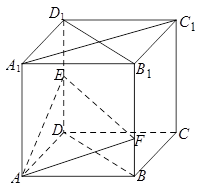
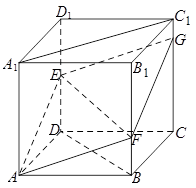
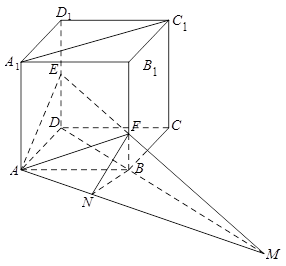
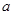 的正方体
的正方体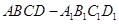 中,点
中,点 是棱
是棱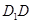 的中点,点
的中点,点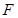 在棱
在棱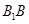 上,且满足
上,且满足 .
.
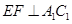 ;
;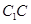 上确定一点
上确定一点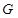 ,使
,使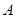 、
、 、
、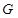 、
、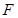 四点共面,并求此时
四点共面,并求此时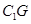 的长;
的长; 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值. ;(3)
;(3)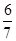 .
.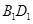 ,先由正方体的性质得到
,先由正方体的性质得到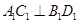 ,以及
,以及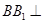 平面
平面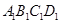 ,从而得到
,从而得到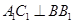 ,利用直线与平面垂直的判定定理可以得到
,利用直线与平面垂直的判定定理可以得到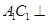 平面
平面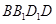 ,于是得到
,于是得到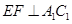 ;(2)假设四点
;(2)假设四点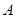 、
、 、
、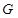 、
、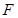 四点共面,利用平面与平面平行的性质定理得到
四点共面,利用平面与平面平行的性质定理得到 ,
, ,于是得到四边形
,于是得到四边形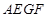 为平行四边形,从而得到
为平行四边形,从而得到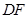 的长度,再结合勾股定理得到
的长度,再结合勾股定理得到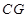 的长度,最终得到
的长度,最终得到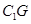 的长度;(3)先延长
的长度;(3)先延长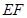 、
、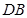 交于点
交于点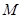 ,连接
,连接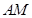 ,找出由平面
,找出由平面 与平面
与平面 所形成的二面角的棱
所形成的二面角的棱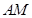 ,借助
,借助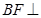 平面
平面 ,从点
,从点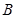 在平面
在平面 内作
内作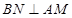 ,连接
,连接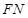 ,利用三垂线法得到
,利用三垂线法得到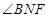 为平面
为平面 与平面
与平面 所形成的二面角的的平面角,然后在直角
所形成的二面角的的平面角,然后在直角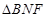 中计算
中计算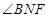 的余弦值;
的余弦值;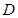 为坐标原点,
为坐标原点, 、
、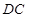 、
、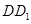 所在直线分别为
所在直线分别为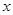 轴、
轴、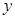 轴、
轴、 轴建立空间直角坐标系,确定
轴建立空间直角坐标系,确定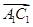 与
与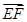 的坐标,利用
的坐标,利用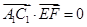 来证明
来证明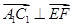 ,进而证明
,进而证明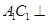
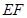 ;(2)先利用平面与平面平行的性质定理得到
;(2)先利用平面与平面平行的性质定理得到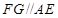 ,然后利用空间向量共线求出点
,然后利用空间向量共线求出点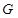 的坐标,进而求出
的坐标,进而求出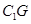 的长度;(3)先求出平面
的长度;(3)先求出平面 和平面
和平面 的法向量,结合图形得到由平面
的法向量,结合图形得到由平面 和平面
和平面 所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.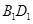 ,
,
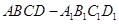 为正方体,所以四边形
为正方体,所以四边形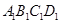 为正方形,所以
为正方形,所以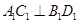 ,
,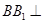 平面
平面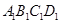 ,
,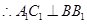 ,
,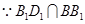 ,
, 平面
平面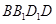 ,
,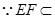 平面
平面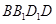 ,
,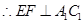 ;
;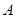 、
、 、
、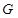 、
、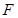 四点共面,则
四点共面,则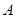 、
、 、
、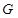 、
、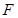 四点确定平面
四点确定平面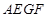 ,
,
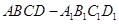 为正方体,所以平面
为正方体,所以平面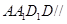 平面
平面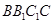 ,
,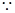 平面
平面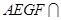 平面
平面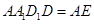 ,平面
,平面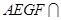 平面
平面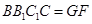 ,
, ,
,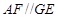 ,因此四边形
,因此四边形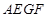 为平行四边形,
为平行四边形,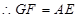 ,
,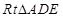 中,
中,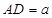 ,
,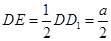 ,
,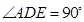 ,
,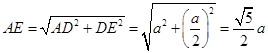 ,
,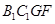 中,下底
中,下底 ,直角腰
,直角腰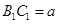 ,斜腰
,斜腰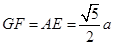 ,
,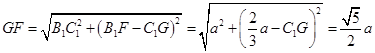 ,
,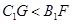 ,解得
,解得 ;
;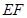 、
、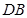 ,设
,设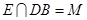 ,连接
,连接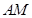 ,则
,则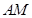 是平面
是平面 与平面
与平面 的交线,
的交线,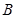 作
作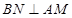 ,垂足为点
,垂足为点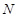 ,连接
,连接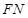 ,
,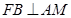 ,
,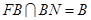 ,所以
,所以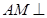 平面
平面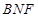 ,
,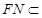 平面
平面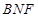 ,所以
,所以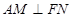 ,
, 为平面
为平面 与平面
与平面 所成二面角的平面角,
所成二面角的平面角,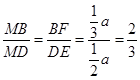 ,即
,即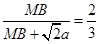 ,因此
,因此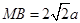 ,
,
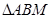 中,
中, ,
,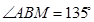 ,
,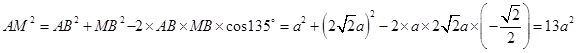 ,
,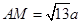 ,
,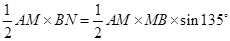 ,
,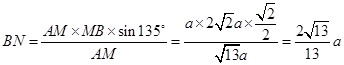 ,
, ,
,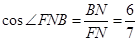 ,故平面
,故平面 与平面
与平面 所成二面角的余弦值为
所成二面角的余弦值为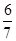 .
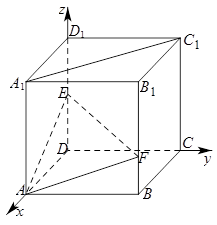
.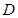 为坐标原点,
为坐标原点, 、
、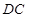 、
、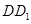 所在直线分别为
所在直线分别为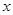 轴、
轴、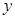 轴、
轴、 轴,建立如下图所示的空间直角坐标系,则
轴,建立如下图所示的空间直角坐标系,则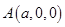 、
、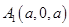 、
、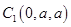 、
、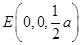 、
、 ,
,
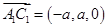 ,
,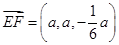 ,因为
,因为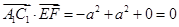 ,
,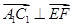 ,所以
,所以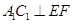 ;
;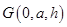 ,因为平面
,因为平面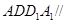 平面
平面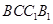 ,
,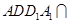 平面
平面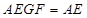 ,平面
,平面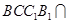 平面
平面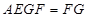 ,所以
,所以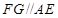 ,
,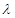 ,使得
,使得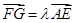 ,
,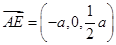 ,
,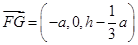 ,所以
,所以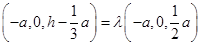 ,
,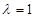 ,
,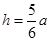 ,所以
,所以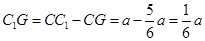 ,
, 时,
时,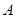 、
、 、
、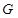 、
、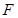 四点共面;
四点共面;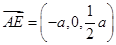 ,
,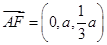 ,
,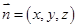 是平面
是平面 的法向量,
的法向量,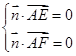 ,即
,即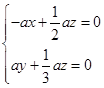 ,
,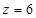 ,则
,则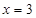 ,
,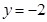 ,所以
,所以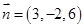 是平面
是平面 的一个法向量,
的一个法向量,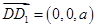 是平面
是平面 的一个法向量,
的一个法向量, 与平面
与平面 所成的二面角为
所成的二面角为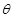 ,
,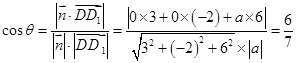 ,
, 与平面
与平面 所成二面角的余弦值为
所成二面角的余弦值为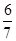 ;
;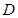 为坐标原点,
为坐标原点, 、
、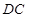 、
、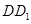 所在直线分别为
所在直线分别为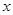 轴、
轴、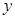 轴、
轴、 轴,建立如下图所示的空间直角坐标系,则
轴,建立如下图所示的空间直角坐标系,则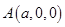 、
、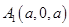 、
、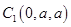 、
、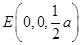 、
、 ,
,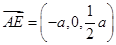 ,
,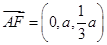 ,
,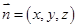 是平面
是平面 的法向量,
的法向量,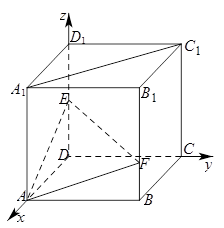
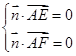 ,即
,即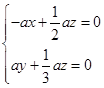 ,
,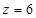 ,则
,则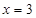 ,
,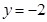 ,所以
,所以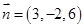 是平面
是平面 的一个法向量,
的一个法向量,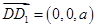 是平面
是平面 的一个法向量,
的一个法向量, 与平面
与平面 所成的二面角为
所成的二面角为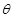 ,
, ,
, 与平面
与平面 所成二面角的余弦值为
所成二面角的余弦值为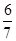 ;
;

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.AB∥CD |
| B.AB与CD异面 |
| C.AB与CD相交 |
| D.AB∥CD或AB与CD异面或AB与CD相交 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若m∥α,n∥α,则m∥n |
| B.若m∥α,m∥β,则α∥β |
| C.若m∥n,m⊥α,则n⊥α |
| D.若m∥α,α⊥β,则m⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com