
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成
年龄段的人员进行了调查研究,将各年龄段人数分成![]() 组:
组:![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
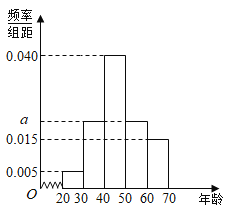
(1)求图中的![]() 值;
值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取![]() 人,则三个组中各抽取多少人?
人,则三个组中各抽取多少人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,则这
人,则这![]() 人都来自于第三组的概率是多少?
人都来自于第三组的概率是多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据频率和为![]() ,即所有小长方形面积和为
,即所有小长方形面积和为![]() ,列出方程,解出
,列出方程,解出![]() 即可.
即可.
(2)第二组、第三组、第四组的频率比为![]() ,由分层抽样能求出三个组依次抽取的人数.
,由分层抽样能求出三个组依次抽取的人数.
(3)在(2)中抽取的![]() 人中,来自于第三组的有
人中,来自于第三组的有![]() 人,用列举法列出所有的基本事件数和抽取的
人,用列举法列出所有的基本事件数和抽取的![]() 人都来自于第三组的事件数,由古典概型求概率即可.
人都来自于第三组的事件数,由古典概型求概率即可.
(1)由频率分布直方图的性质可得![]() ,解得
,解得![]() .
.
(2)第二组、第三组、第四组的频率比为![]() ,共抽取
,共抽取![]() 人,
人,
所以三个组依次抽取的人数为![]() .
.
(3)记第二组![]() 人分别为
人分别为![]() ,第三组
,第三组![]() 人分别为
人分别为![]() ,
,
第四组![]() 人分别为
人分别为![]() .
.
从![]() 人中抽取两人共包含
人中抽取两人共包含
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,共
,共![]() 个基本事件.
个基本事件.
而两人都来自于第三组的基本事件包括
![]() ,
,![]() ,
,![]() ,共
,共![]() 个.
个.
故所求概率为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 轴,
轴,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为
为![]() 椭圆上一点,且
椭圆上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程及
的方程及![]() 的值;
的值;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围.
的离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,![]() 成等差数列,其公差为
成等差数列,其公差为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明
,证明![]() 成等比数列(
成等比数列(![]() );
);
(3)若对任意![]() ,
,![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,设
,设![]() ,证明数列
,证明数列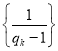 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,右焦点
,右焦点![]() 的坐标为
的坐标为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点(直线不与
两点(直线不与![]() 轴垂直),已知点
轴垂直),已知点![]() 与点
与点![]() 关于
关于![]() 轴对称,证明:直线
轴对称,证明:直线![]() 恒过定点,并求出此定点坐标.
恒过定点,并求出此定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过年时小明的舅舅在家庭微信群里发了一个10元的红包,红包被随机分配为2.51元,3.32元,1.24元,0.26元,2.67元,共五份.现已知小明与爸爸都各自抢到了一个红包,则两人抢到红包的金额总和不小于4元的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com