Question

【题目】某小区提倡低碳生活，环保出行，在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用，管理这些自行车的费用是每日92元，根据经验，若每辆自行车的日租金不超过5元，则自行车可以全部出租，若超过5元，则每超过1元，租不出的自行车就增加2辆，为了便于结算，每辆自行车的日租金元只取整数，用元表示出租自行车的日纯收入（日纯收入=一日出租自行车的总收入-管理费用）

（1）求函数的解析式及其定义域；

（2）当租金定为多少时，才能使一天的纯收入最大？

Answer 1

【答案】（1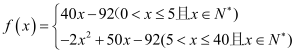），其定义域为，（2）定价为12或13，一天的纯收入最大，最大值为220元.

【解析】

试题分析：（1）设日租金为元（），当时，一日出租自行车总收入为元，则此时，当时，一日出租自行车总收入为，则此时，因此函数的为分段函数，则函数的解析式为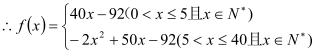；（2）本问考查求分段函数的最大值，当且时，，函数单调递增，所以当时元，当且时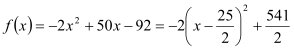， ，根据二次函数图象及性质可知，当或13时，因为220>108，所以函数的最大值为220，此时定价为12或13.

试题解析：（1）由题意：当且时，

当且时，

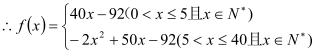
其定义域为

（2）当且时，

当时（元）

当且时，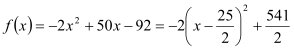

开口向下，对称轴为，又

当或13时（元）

当租金定为12元或13元时，

一天的纯收入最大为220元