
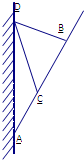
 某固定在墙上的广告金属支架如图所示,根据要求,AB长要超过4米(不含4米),C为AB的中点,B到D的距离比CD的长小1米,∠BCD=60°
某固定在墙上的广告金属支架如图所示,根据要求,AB长要超过4米(不含4米),C为AB的中点,B到D的距离比CD的长小1米,∠BCD=60°分析 (1)根据题意,CD=x,则BD=(x-1)m,设CB=y,那么支架的总长度为AC+BC+BD+CD,利用余弦定理把各边长关系建立起来,可得总长度表示为y的函数.
(2)根据(1)中的总长度y的函数关系式,利用基本不等式的性质求解最小值.即支架最短总长度.
解答 解:(1)根据题意,由CD=x,则BD=(x-1)m,C为AB的中点,AC=BC,设CB=y.
则支架的总长度为AC+BC+BD+CD,则总长度l=2y+2x+1.
在△CBD中,由余弦定理可得:x2+y2-2xycos60°=(x-1)2,
化简得:y2-xy+2x-1=0,
则$x=\frac{{{y^2}-1}}{y-2}$,
总长度$l=2y+2×\frac{{{y^2}-1}}{y-2}-1=2y+\frac{{2{y^2}-2}}{y-2}-1$,
由题中条件得2y>4,即y>2.
(2)由(1)可得:总长度l=$\frac{2{y}^{2}-2}{y-2}+2y-1$,(y>2),
设y-2=t(t>0),
则总长度$l=2•\frac{{{{({t+2})}^2}-1}}{t}-2({t+2})-1=2({t+4+\frac{3}{t}})+2t+3=4t+\frac{6}{t}+11$,
∵t>0
由基本不等式可知:$4t+\frac{6}{t}≥4\sqrt{6}$,
有且仅当4t2=6,即$t=\frac{{\sqrt{6}}}{2}$时成立,
又由$t=\frac{{\sqrt{6}}}{2}$,满足t>0.
∴$y=\frac{{\sqrt{6}}}{2}+2$,
∴$x=\frac{{3\sqrt{6}+8}}{2}$,
∴当$AB=\sqrt{6}+4,CD=\frac{{8+3\sqrt{6}}}{2}$时,金属支架总长度最短.
点评 本题考查了余弦定理在实际生活中的运用能力和计算能力,注意定义域的问题.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12 | B. | $\sqrt{74}$ | C. | $\sqrt{80}$ | D. | $3\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {2,4,5,6,7,8} | C. | {5,6,7} | D. | {4,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com