
【题目】已知椭圆C:![]() 的左焦点为F(﹣1,0),离心率为
的左焦点为F(﹣1,0),离心率为![]() ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F不与坐标轴垂直的直线交椭圆C于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
【答案】![]() 1;(Ⅱ)(
1;(Ⅱ)(![]() ,0)
,0)
【解析】
(Ⅰ)由题意可知:c=1,a2=b2﹣c2,e![]() ,由此求出椭圆的方程.(II)设直线AB的方程为y=k(x+1)(k≠0),联立方程,得(1+2k2)x2+4k2x+2k2﹣2=0.由直线AB过椭圆的左焦点F,记A(x1,y1),B(x2,y2),AB的中点N(x0,y0),x1+x2
,由此求出椭圆的方程.(II)设直线AB的方程为y=k(x+1)(k≠0),联立方程,得(1+2k2)x2+4k2x+2k2﹣2=0.由直线AB过椭圆的左焦点F,记A(x1,y1),B(x2,y2),AB的中点N(x0,y0),x1+x2![]() ,x0
,x0![]() ,垂直平分线NG的方程为y﹣y0
,垂直平分线NG的方程为y﹣y0![]() ,由此能求出点G横坐标的取值范围.
,由此能求出点G横坐标的取值范围.
(Ⅰ)由题意可知:c=1,a2=b2﹣c2,e![]()
解得:a![]() ,b=1
,b=1
故椭圆的方程为:![]() 1
1
(II)设直线AB的方程为y=k(x+1)(k≠0),
与椭圆联立,得(1+2k2)x2+4k2x+2k2﹣2=0
∵直线AB过椭圆的左焦点F∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB的中点N(x0,y0)
则x1+x2![]()
x0![]()
垂直平分线NG的方程为y﹣y0![]() ,
,
令y=0,得xG=x0+ky0![]()
![]() .
.
∵k≠0,∴![]() 0
0
∴点G横坐标的取值范围为(![]() ,0).
,0).


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点![]() 到两坐标轴的距离之和等于它到定点
到两坐标轴的距离之和等于它到定点![]() 的距离,记点P的轨迹为
的距离,记点P的轨迹为![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 关于原点对称;②
关于原点对称;②![]() 关于直线
关于直线![]() 对称;③直线
对称;③直线![]() 与
与![]() 有无数个公共点;④在第一象限内,
有无数个公共点;④在第一象限内,![]() 与x轴和y轴所围成的封闭图形的面积小于
与x轴和y轴所围成的封闭图形的面积小于![]() .其中正确的结论是________.(写出所有正确结论的序号)
.其中正确的结论是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海湿地如图所示,A、B和C、D分别是以点O为中心在东西方向和南北方向设置的四个观测点,它们到点O的距离均为![]() 公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
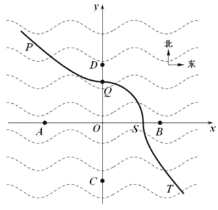
(1)求观光长廊PQST所在的曲线的方程;
(2)在观光长廊的PQ段上,需建一服务站M,使其到观测点A的距离最近,问如何设置服务站M的位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司推出一新款手机,因其功能强大,外观新潮,一上市便受到消费者争相抢购,销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.
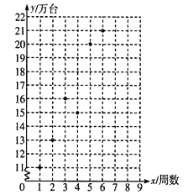
(Ⅰ)根据散点图,用最小二乘法求![]() 关于
关于![]() 的线性回归方程,并预测该款手机第8周的销量;
的线性回归方程,并预测该款手机第8周的销量;
(Ⅱ)为了分析市场趋势,该公司市场部从前6周的销售数据中随机抽取2周的数据,求抽到的这2周的销量均在20万台以下的概率.
参考公式:回归直线方程![]() ,其中:
,其中: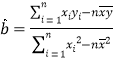 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() ,点
,点![]() 为线段
为线段![]() 的中点,且
的中点,且![]()
![]() .
. ![]() ,
, ![]() .现将△
.现将△![]() 沿
沿![]() 进行翻折,使得
进行翻折,使得![]()
![]() °,得到图形如图所示,连接
°,得到图形如图所示,连接![]() .
.
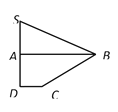
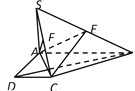
(Ⅰ)若点![]() 在线段
在线段![]() 上,证明:
上,证明: ![]() ;
;
(Ⅱ)若![]() 点为
点为![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com