考点:数列与不等式的综合
专题:计算题,等差数列与等比数列,不等式的解法及应用
分析:(1)当n≥2时,an=Sn-Sn-1=nan-(n-1)an-1-2(n-1),易证an-an-1=2(n≥2,n∈N*),于是可得:{an}是等差数列,再由等差数列的通项公式,即可得到通项,再由裂项相消求和,求得Tn;
(2)分别讨论n为奇数和偶数,运用分离参数,讨论右边的最小值,注意运用单调性和基本不等式,即可得到范围.
解答:
解:(1)当n≥2,n∈N
*时,由已知S
n=na
n-n(n-1)
得S
n-1=(n-1)a
n-1-(n-1)(n-2).
两式相减得S
n-S
n-1=na
n-(n-1)a
n-1-2(n-1).
又S
n-S
n-1=a
n,所以(n-1)a
n-(n-1)a
n-1=2(n-1).
即a
n-a
n-1=2(n≥2,n∈N
*).
所以{a
n}是以1为首项、2为公差的等差数列,
即a
n=1+2(n-1)=2n-1,
b
n=
=
=
(
-).
则T
n=b
1+b
2+…+b
n=
[(1
-)+(
-)+…+(
-)]
=
(1-
).
则T
n=
;
(2)由于对任意的n∈N
+,不等式λT
n<n+8(-1)
n恒成立,
则当n为奇数时,有λT
n<n-8恒成立,
即有
λ<=2n-
-15,
由于2n-
-15在n≥1上递增,则n=1取得最小值,且为-21,
则λ<-21;
当n为偶数时,有λT
n<n+8恒成立,
即有
λ<=2n+
+17,
由于2n+
+17≥2
+17=25,当且仅当n=2,取得最小值,且为25.
则λ<25.
由于对任意的n∈N
+,不等式恒成立,则λ<-21.
则实数λ的取值范围是(-∞,-21).
点评:本题考查数列的通项和求和,着重考查运算、推理的能力,突出考查等差关系的确定与裂项法求和的综合应用,属于中档题.



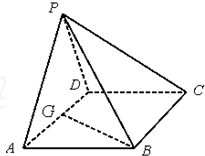 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.