
分析 设出A、B两点的坐标,由线段的中点公式求出A、B两点的坐标,用两点式求直线的方程,并化为一般式.
解答 解:设A(a,b)、B(m,n),
∵点P(2,1)为线段AB的中点,
∴a+m=4.b+n=2,
∴m=4-a,n=2-b,
由A,B点分别是直线l与直线l1:2x-y-1=0与l2:x+y+2=0的交点,
故$\left\{\begin{array}{l}2a-b-1=0\\(4-a)+(2-b)+2=0\end{array}\right.$
解得:a=3,b=5,即A点坐标为(3,5)
∴直线l的方程为:$\frac{y-1}{5-1}=\frac{x-2}{3-2}$,
即4x-y-7=0.
点评 本题考查线段的中点公式的应用,用两点式求直线的方程.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 60°或120° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源:2017届广西陆川县中学高三9月月考数学(文)试卷(解析版) 题型:解答题
如图,三棱柱 的侧棱
的侧棱 底面
底面 ,
,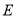 是棱
是棱 的中点,
的中点, 是
是 的中点,
的中点, .
.

(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
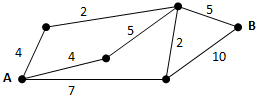 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com