已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1)平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)设直线MA、MB的斜率分别为k1,k2,求证k1+k2=0.
【答案】
分析:(1)先设出椭圆的标准方程,根据题意联立方程组,求得a和b,椭圆的方程可得.
(2)由点斜式设出直线l的方程与椭圆方程联立消去y,根据判别式大于0求得k的范围.
(3)设A(x
1,y
1),B(x
2,y
2)由根据韦达定理,分别求得x
1+x
2和x
1x
2进而表示出k
1和k
2,进而可求得k
1+k
2.
解答:解:(1)设椭圆方程为
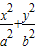
=1
则
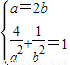
解得a
2=8,b
2=2
∴椭圆方程为
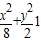
(2)∵直线l平行与OM,且在一轴上的截距为m,由k
OM=

∴l的方程为y=

x+m
由直线方程与椭圆方程联立消去y得x
2+2mx+2m
2-4=0
∵直线l与椭圆交与A,B两个不同点
∴△=(2m)
2-4(2m
2-4)>0
解得-2<m<2,且m≠0
(3)设A(x
1,y
1),B(x
2,y
2)
由x
2+2mx+2m
2-4=0可得
x
1+x
2=-2m,x
1x
2=2m
2-4
则k
1=
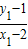
,k
2=
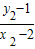
而k
1+k
2=
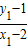
+
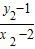
=
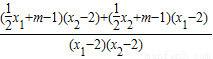
=
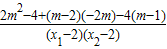
=0
∴k
1+k
2=0,
故得证.
点评:本题主要考查了椭圆的应用.考查了学生综合分析问题和解决问题的能力.

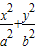 =1
=1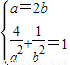 解得a2=8,b2=2
解得a2=8,b2=2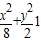

 x+m
x+m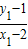 ,k2=
,k2=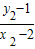
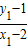 +
+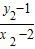 =
=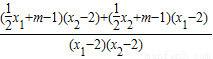 =
=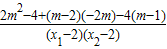 =0
=0
