

(1)侧面与底面所成角;
(2)相邻两个侧面所成的二面角.
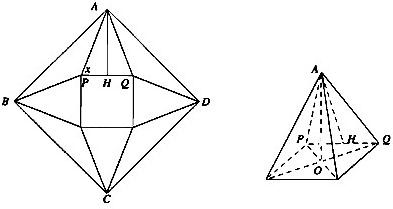
解析:(1)如题图,O为正方形的中心,SO⊥平面ABCD,SE⊥BC,∴OE⊥BC.?
∴∠SEO为侧面SBC与底面ABCD所成角的平面角.?
∵SB=SC=BC=a,∴OE=![]() ,SE=
,SE=![]() .?
.?
在Rt△SOE中,cos∠SEO=![]() ,?
,?
∴∠SEO=arccos![]() ,?
,?
即侧面与底面所成角的大小为arccos![]() .?
.?
(2)过B点作BF⊥AS,垂足为F,连结DF、BD.?
∵△ABS≌△ADS,∴DF⊥AS.?
∴∠BFD为相邻两个侧面所成的二面角的平面角.?
在△BDF中,BD=![]() ,BF=DF=
,BF=DF=![]() .?
.?
由余弦定理得?
cos∠BFD=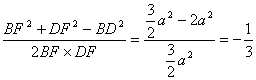 ,?
,?
∴∠BFD=π-arccos![]() ,?
,?
即相邻两个侧面所成的二面角的大小为π-arccos![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高二上学期期中考试理数试卷(解析版) 题型:选择题
如图,正四棱锥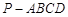 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
A.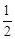 B.
B.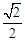
C.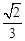 D.
D.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江高二上学期期中考试理科数学试卷(解析版) 题型:选择题
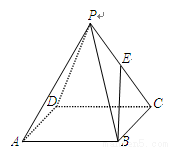
( )如图,正四棱锥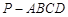 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
A. B.
B.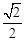 C.
C.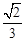 D.
D.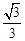
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com