
【题目】已知函数![]() .
.
(1)![]() 时,求
时,求![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)![]() 且
且![]() ,
, ![]() 均恒成立,求实数
均恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)求出![]() ,令
,令![]() 在
在![]() 内求得
内求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,令
增区间,令![]() 在
在![]() 内求得
内求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)
的减区间;(2)![]() 时,
时, ![]() ,即
,即![]() ;
; ![]() 时,
时, ![]() ,即
,即![]() , 设
, 设![]() ,分两种情况研究函数的单调性,并求出
,分两种情况研究函数的单调性,并求出![]() 的最值,从而可得实数
的最值,从而可得实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 时,
时, ![]() ,设
,设![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上是单调递减函数,即则
上是单调递减函数,即则![]() 在
在![]() 上是单调递减函数,
上是单调递减函数,
∵![]() ∴
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]()
∴在![]() 上
上![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ;
;
(2)![]() 时,
时, ![]() ,即
,即![]() ;
;
![]() 时,
时, ![]() ,即
,即![]() ;
;
设![]()
则![]()
![]() 时,
时, ![]() ,∵
,∵![]() ,∴
,∴ ![]() 在
在![]() 上单调递增
上单调递增
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,∴
,∴ ![]() 符合题意;
符合题意;
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,∴
,∴ ![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时, ![]() ,与
,与![]() 时,
时, ![]() 矛盾;舍
矛盾;舍
![]() 时,设
时,设![]() 为
为![]() 和0中的最大值,当
和0中的最大值,当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,∴当
上单调递减,∴当![]() 时,
时, ![]() ,与
,与![]() 时,
时, ![]() 矛盾;舍
矛盾;舍
综上, ![]()


科目:高中数学 来源: 题型:
【题目】(导学号:05856308)(12分)
如图,∠ABC=![]() ,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
(Ⅰ)求证:平面PBD⊥平面COD;
(Ⅱ)求点O到平面BDC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018四川绵阳南山中学高三二诊热身考试】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩![]() 服从正态分布
服从正态分布![]() ,已知
,已知![]() ,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;
,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;
②已知命题![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
③在![]() 上随机取一个数
上随机取一个数![]() ,能使函数
,能使函数![]() 在
在![]() 上有零点的概率为
上有零点的概率为![]() ;
;
④在某次飞行航程中遭遇恶劣气候,用分层抽样的20名男乘客中有5名晕机,12名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用独立性检验,有97%以上的把握认为与性别有关.
| 0.15 | 0.1 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
其中真命题的序号为( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:关于x的二次方程x2+(a+1)x+a-2=0的一个根大于零,另一根小于零;命题q:不等式2x2+x>2+ax对x∈(-∞,-1)恒成立.如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() , 若椭圆上一点
, 若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 是点
是点![]() 在
在![]() 轴上的垂足,延长
轴上的垂足,延长![]() 交椭圆
交椭圆![]() 于
于![]() ,求证:
,求证: ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
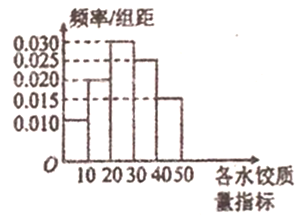
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
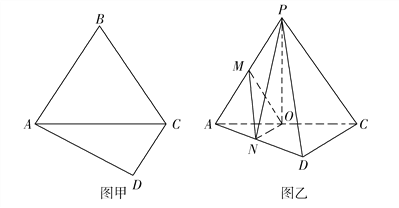
【题目】如图甲,在四边形ABCD中, ![]() ,
, ![]() 是边长为4的正三角形,把
是边长为4的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面PAC
的位置,使得平面PAC![]() 平面ACD,如图乙所示,点
平面ACD,如图乙所示,点![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com