
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() , 若椭圆上一点
, 若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 是点
是点![]() 在
在![]() 轴上的垂足,延长
轴上的垂足,延长![]() 交椭圆
交椭圆![]() 于
于![]() ,求证:
,求证: ![]() 三点共线.
三点共线.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】(导学号:05856295)德国大数学家高斯年少成名,被誉为数学王子.19岁的高斯得到了一个数学史上非常重要的结论,就是《正十七边形尺规作图之理论与方法》, 在其年幼时,对1+2+3+…+100的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也被称为高斯算法.现有函数f(x)=![]() ,则f(1)+f(2)+…+f(m+2017)等于( )
,则f(1)+f(2)+…+f(m+2017)等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,若f(x)≥2ln x在[1,+∞)上恒成立,则a的取值范围是( )
,若f(x)≥2ln x在[1,+∞)上恒成立,则a的取值范围是( )
A. (1,+∞) B. [1,+∞)
C. (2,+∞) D. [2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 是正方形,二面角
是正方形,二面角![]() 的大小为
的大小为![]() .
.
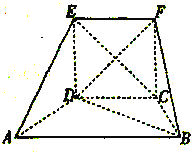
(1)在线段![]() 上找出一点
上找出一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解城市交通压力,某市市政府在市区一主要交通干道修建高架桥,两端的桥墩现已建好,已知这两桥墩相距m米,“余下的工程”只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记“余下工程”的费用为y万元.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记“余下工程”的费用为y万元.
(1)试写出工程费用y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使工程费用y最小?并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF//AE,AB=AE=2.
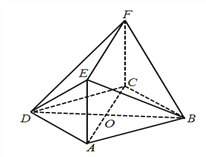
(1)求证:BD⊥平面ACFE;
(2)当直线FO与平面BDE所成的角为45°时,求二面角B﹣EF﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() (
(![]() ,
, ![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,过点
,过点![]() 作圆
作圆![]() :
: ![]() 的切线
的切线![]() ,切点为
,切点为![]() ,且直线
,且直线![]() 与双曲线
与双曲线![]() 的一个交点
的一个交点![]() 满足
满足![]() ,设
,设![]() 为坐标原点,若
为坐标原点,若![]() ,则双曲线
,则双曲线![]() 的渐近线方程为( )
的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com