
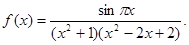 对于下列命题:
对于下列命题: 是周期函数;②函数
是周期函数;②函数 既有最大值又有最小值;
既有最大值又有最小值; 的定义域是
的定义域是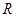 ,且其图象有对称轴;
,且其图象有对称轴;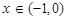 ,函数
,函数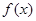 的导函数
的导函数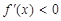 .
.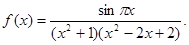 的解析式,它不是一个奇函数,由于分子的值从-1到1周期性变化,分母的值随着x的值远离原点,逐渐趋向于正无穷大,函数图象逐渐靠近x轴,由这些性质对四个命题进行判断选出正确选项
的解析式,它不是一个奇函数,由于分子的值从-1到1周期性变化,分母的值随着x的值远离原点,逐渐趋向于正无穷大,函数图象逐渐靠近x轴,由这些性质对四个命题进行判断选出正确选项

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
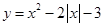 的递增区间为
的递增区间为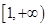 ;④定义在R上的函数
;④定义在R上的函数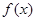 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有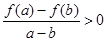 成立,则
成立,则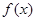 在R上是增函数;⑤
在R上是增函数;⑤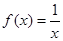 的单调减区间是
的单调减区间是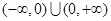 ;正确的有____________
;正确的有____________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com