
(本小题满分14分)已知函数f(x)=ax+ (a>1).
(a>1).
(1)判定函数f(x)在(-1,+∞)上的单调性,并给出证明;
(2)证明方程f(x)=0没有负数根.
科目:高中数学 来源:2014-2015学年广东省高一10月月考数学试卷(解析版) 题型:选择题
设函数f(x)= ,则不等式f(x)>f(1)的解集是( )
,则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一上学期阶段一考试数学试卷(解析版) 题型:选择题
设定义在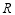 上的函数
上的函数 对任意实数
对任意实数 满足
满足 ,且
,且 ,则
,则 ( )
( )
A.10 B.7 C.4 D.-1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一上学期期初考试数学试卷(解析版) 题型:填空题
设函数 ,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=________,关于x的方程f(x)=x的解的个数为________个.
,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=________,关于x的方程f(x)=x的解的个数为________个.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一上学期期初考试数学试卷(解析版) 题型:选择题
下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),都有 ”的是( )
”的是( )
A.f(x)=ex B.f(x)=(x-1)2 C.f(x)= D.f(x)=︳x+1︳
D.f(x)=︳x+1︳
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省校高一上学期第一次考试数学试卷(解析版) 题型:选择题
已知f ( )=
)= ,则f (x)的解析式为( )
,则f (x)的解析式为( )
A.f(x) = B.f (x)=
B.f (x)= C.f (x)=
C.f (x)= D.f (x)=1+x
D.f (x)=1+x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com