
 已知正四面体ABCD,点E,F分别为AB,CD的中点,边长为2.
已知正四面体ABCD,点E,F分别为AB,CD的中点,边长为2.分析 (1取BD中点G,则FG∥BC,∠AFE是BC与AF所成的角(或所成角的补角),由此能求出BC与AF所成的角的余弦值.
(2)取BC中点P,则AP⊥BC,DP⊥BC,BC⊥平面APD,由此能求出BC与AD所成的角.
(3)取BF中点O,连结EO,CO,则EO∥AF,∠CEO是CE与AF所成角(或所成角的补角),由此能求出CE与AF所成角余弦值.
解答 解:(1)取BD中点G,连结AG、FG、AF,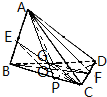
则FG∥BC,∴∠AFE是BC与AF所成的角(或所成角的补角),
∵AG=AF=$\sqrt{4-1}$=$\sqrt{3}$,FG=1,
∴cos∠AFE=$\frac{A{F}^{2}+F{G}^{2}-A{G}^{2}}{2AF•GF}$=$\frac{3+1-3}{2•\sqrt{3}•1}$=$\frac{\sqrt{3}}{6}$,
∴BC与AF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
(2)取BC中点P,连结AP、DP,
则AP⊥BC,DP⊥BC,且AP∩DP=P,
∴BC⊥平面APD,
又AD?平面APD,∴BC⊥AD,
∴BC与AD所成的角为90°.
(3)取BF中点O,连结EO,CO,则EO∥AF,
∴∠CEO是CE与AF所成角(或所成角的补角),
∵OE=$\frac{AF}{2}=\frac{\sqrt{3}}{2}$,CE=$\sqrt{3}$,CO=$\sqrt{C{F}^{2}+(\frac{BF}{2})^{2}}$=$\sqrt{1+\frac{3}{4}}$=$\frac{\sqrt{7}}{2}$,
∴cos∠CEO=$\frac{C{E}^{2}+O{E}^{2}-C{O}^{2}}{2•CE•OE}$=$\frac{3+\frac{3}{4}-\frac{7}{4}}{2•\sqrt{3}•\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$,
∴CE与AF所成角余弦值为$\frac{2}{3}$.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,一个圆柱形乒乓球筒,高为40厘米,底面半径为4厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.
如图所示,一个圆柱形乒乓球筒,高为40厘米,底面半径为4厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com