
分析 (1)利用一元二次方程的根与系数的关系可得:$\frac{{b}^{2}}{{a}^{2}}$-2×$\frac{c}{a}$=10,根据二次函数的性质可得:$-\frac{b}{2a}$=-2,c=3,联立检查即可得出.
(2)ax2+bx+c=3,即x2+4x+3=3,可得A={0,-4}.根据B⊆A,可得B=∅,{0},{-4},{0,-4}.利用一元二次方程的根与系数及其判别式的关系即可得出.
解答 解:(1)设方程f(x)=0的两个实根分别为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,∵${x}_{1}^{2}+{x}_{2}^{2}$=10,∴$({x}_{1}+{x}_{2})^{2}$-2x1•x2=$\frac{{b}^{2}}{{a}^{2}}$-2×$\frac{c}{a}$=10,又$-\frac{b}{2a}$=-2,c=3,
联立解得:c=3,a=1,b=4.
(2)ax2+bx+c=3,即x2+4x+3=3,化为x2+4x=0,解得:x=0,-4,∴A={0,-4}.
∵B⊆A,∴B=∅,或B={0},或B={-4},或B={0,-4}.
①B=∅时,△=4(m+1)2-4(m2-1)<0,解得:m<-1;
②B={0},则$\left\{\begin{array}{l}{△=0}\\{{m}^{2}-1=0}\end{array}\right.$,解得m=-1.
③B={-4},则$\left\{\begin{array}{l}{△=0}\\{16-8(m+1)+{m}^{2}-1=0}\end{array}\right.$,解得:m∈∅.
④B={0,-4},则$\left\{\begin{array}{l}{0-4=-(m+1)}\\{0×(-4)={m}^{2}-1}\end{array}\right.$,△>0,联立解得m∈∅.
综上可得:实数m的取值范围是(-∞,-1].
点评 本题考查了二次函数的性质、一元二次方程的根与系数及其判别式的关系、集合之间的关系,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
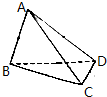 已知正四面体ABCD,点E,F分别为AB,CD的中点,边长为2.
已知正四面体ABCD,点E,F分别为AB,CD的中点,边长为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
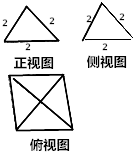
| A. | 4+4$\sqrt{3}$cm2,$\frac{16\sqrt{3}}{3}$cm3 | B. | 4+4$\sqrt{3}$cm2,$\frac{16\sqrt{2}}{3}$cm3 | C. | 12cm2,$\frac{16\sqrt{3}}{3}$cm3 | D. | 12cm2,$\frac{16\sqrt{2}}{3}$cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果一条直线与两条平行线中的一条相交,则必与另一条相交 | |
| B. | 如果两条直线同时与第三条直线垂直,则这两条直线平行 | |
| C. | 如果两条直线同时与第三条直线相交,则这两条直线相交 | |
| D. | 如果一条直线与两条平行线中的一条垂直,则必与另一条垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com