
分析 (1)求得椭圆的a,b,c,可得左右焦点,设P(x,y)(x>0,y>0),运用向量的数量积的坐标表示,解方程可得P的坐标;
(2)显然x=0不满足题意,可设l的方程为y=kx+2,设A(x1,y1),B(x2,y2),联立直线方程和椭圆方程,运用韦达定理和判别式大于0,由∠AOB为锐角,即为$\overrightarrow{OA}•\overrightarrow{OB}>0$,运用数量积的坐标表示,解不等式即可得到所求k的范围.
解答 解:(1)因为椭圆方程为$\frac{x^2}{4}+{y^2}=1$,
知a=2,b=1,$c=\sqrt{3}$,
可得${F_1}(-\sqrt{3},0)$,${F_2}(\sqrt{3},0)$,
设P(x,y)(x>0,y>0),
则$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=(-\sqrt{3}-x,-y)•(\sqrt{3}-x,-y)={x^2}+{y^2}-3=-\frac{5}{4}$,
又$\frac{x^2}{4}+{y^2}=1$,联立$\left\{{\begin{array}{l}{{x^2}+{y^2}=\frac{7}{4}}\\{\frac{x^2}{4}+{y^2}=1}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{{x^2}=1}\\{{y^2}=\frac{3}{4}}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=1}\\{y=\frac{{\sqrt{3}}}{2}}\end{array}}\right.$,即为$P(1,\frac{{\sqrt{3}}}{2})$;
(2)显然x=0不满足题意,可设l的方程为y=kx+2,
设A(x1,y1),B(x2,y2),
联立$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=kx+2}\end{array}}\right.⇒(1+4{k^2}){x^2}+16kx+12=0$,
由△=(16k)2-4(1+4k2)•12>0,得${k^2}>\frac{3}{4}$.
${x_1}+{x_2}=-\frac{16k}{{1+4{k^2}}}$,${x_1}{x_2}=\frac{12}{{1+4{k^2}}}$.
又∠AOB为锐角,即为$\overrightarrow{OA}•\overrightarrow{OB}>0$,
即x1x2+y1y2>0,x1x2+(kx1+2)(kx2+2)>0,
又$(1+{k^2}){x_1}{x_2}+2k({x_1}+{x_2})+4=(1+{k^2})\frac{12}{{1+4{k^2}}}+2k(-\frac{16k}{{1+4{k^2}}})+4=\frac{{4(4-{k^2})}}{{1+4{k^2}}}>0$,
可得k2<4.又${k^2}>\frac{3}{4}$,即为$\frac{3}{4}<{k^2}<4$,
解得$k∈(-2,-\frac{{\sqrt{3}}}{2})∪(\frac{{\sqrt{3}}}{2},2)$.
点评 本题考查椭圆方程的运用,向量的数量积的坐标表示,考查直线方程和椭圆方程联立,运用判别式大于0和韦达定理,以及角为锐角的条件:数量积大于0,考查解方程和解不等式的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
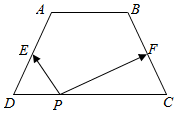 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,那么实数λ的取值范围为(-$\frac{9}{20}$,-$\frac{1}{4}$).
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,那么实数λ的取值范围为(-$\frac{9}{20}$,-$\frac{1}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
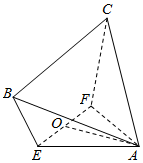 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com