
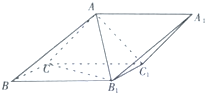
 如图,在三棱柱ABC-A1B1C1中,△ACC1≌△B1 CC1,CA⊥C1 A且CA=C1 A=2.
如图,在三棱柱ABC-A1B1C1中,△ACC1≌△B1 CC1,CA⊥C1 A且CA=C1 A=2.分析 (Ⅰ)连AC1,CB1,证明CC1⊥OA,CC1⊥OB1,推出CC1⊥平面OAB1,然后证明CC1⊥AB1.
(Ⅱ)说明OA⊥平面BB1C1C.求出${S_{四形B{B_1}{C_1}C}}$,然后求解四棱锥A-BCC1B1的体积.
解答  解:(Ⅰ)证明:连AC1,CB1,则△ACC1和△B1CC1均为等腰直角三角形.
解:(Ⅰ)证明:连AC1,CB1,则△ACC1和△B1CC1均为等腰直角三角形.
取CC1中点O,连OA,OB1,则:
CC1⊥OA,CC1⊥OB1,
则CC1⊥平面OAB1,…(4分)
所以CC1⊥AB1. …(6分)
(Ⅱ)解:由(Ⅰ)知,OA=OB1=$\sqrt{2}$,又AB1=2,
所以OA⊥OB1.又OA⊥CC1,OB1∩CC1=O,
所以OA⊥平面BB1C1C.${S_{四形B{B_1}{C_1}C}}$=BC×BB1=4.
所以${V_{A-B{B_1}{C_1}C}}=\frac{1}{3}×4×\sqrt{2}=\frac{{4\sqrt{2}}}{3}$.…(12分)
点评 本题考查直线与平面垂直的判定定理,平面与平面垂直的性质定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | $(\frac{π}{3},0)$ | C. | $(\frac{π}{6},0)$ | D. | $(\frac{π}{9},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-5)2+(y-3)2=18 | B. | (x-5)2+(y-3)2=9 | C. | (x-3)2+(y-5)2=18 | D. | (x-3)2+(y-5)2=9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com