
分析 由复合函数的单调性可得f(x)在定义域上为单调增函数,结合函数f(x)=x+ln$\sqrt{x}$在区间[a,b]的值域为[ta,tb],可得ln$\sqrt{a}$+a=ta,ln$\sqrt{b}$+b=tb,即a,b为方程ln$\sqrt{x}$+x=tx的两个不同根.即t=1+$\frac{ln\sqrt{x}}{x}$有两个不同根,令g(x)=1+$\frac{ln\sqrt{x}}{x}$,利用导数研究其单调性并求得极值,数形结合可得t的取值范围.
解答 解:∵f(x)=x+ln$\sqrt{x}$的定义域为{x|x>0},f(x)在定义域上为单调增函数,
又函数f(x)=x+ln$\sqrt{x}$在区间[a,b]的值域为[ta,tb],
∴f(a)=ta,f(b)=tb,
即:ln$\sqrt{a}$+a=ta,ln$\sqrt{b}$+b=tb,即a,b为方程ln$\sqrt{x}$+x=tx的两个不同根.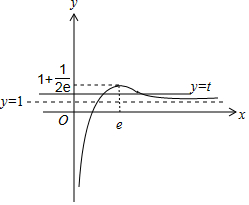
∴t=1+$\frac{ln\sqrt{x}}{x}$有两个不同根,
令g(x)=1+$\frac{ln\sqrt{x}}{x}$,则g'(x)=$\frac{\frac{1}{2}•\frac{1}{\sqrt{x}}•\frac{1}{\sqrt{x}}•x-ln\sqrt{x}}{{x}^{2}}$=$\frac{\frac{1}{2}-ln\sqrt{x}}{{x}^{2}}$,
由g′(x)=0,得$\frac{1}{2}-ln\sqrt{x}=0$,得x=e.
∴当x∈(0,e)时,g′(x)>0,当x∈(e,+∞)时,g′(x)<0,
∴g(x)在(0,e)上为增函数,在(e,+∞)上为减函数.
可得极大值点x=e,故g(x)的极大值为:g(e)=1+$\frac{1}{2e}$,
又当x→0+时,g(x)→-∞,当x→∞时,g(x)→1,
因此当1<t<1+$\frac{1}{2e}$时,直线y=t与曲线y=g(x)的图象有两个交点,方程 t=1+$\frac{lnx}{x}$有两个解.
故所求的t的取值范围为(1,1+$\frac{1}{2e}$),
故答案为:(1,1+$\frac{1}{2e}$).
点评 本题考查利用导数研究函数的单调性,考查根的存在性及根的个数判断,体现了数学转化思想方法与数形结合的解题思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移y(单位:cm)随时间t(单位:s)的变化曲线如图所示,则小球在开始振动(即t=0)时离开平衡位置的位移是3$\sqrt{3}$.
弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移y(单位:cm)随时间t(单位:s)的变化曲线如图所示,则小球在开始振动(即t=0)时离开平衡位置的位移是3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $2\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | $3+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -26 | B. | -27 | C. | -28 | D. | -29 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},1}]$ | B. | [1,2] | C. | $[{0,\frac{1}{2}}]$ | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -18 | B. | -6 | C. | 0 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com