
| A. | 1 | B. | 8 | C. | 9 | D. | 2$\sqrt{2}$ |
分析 运用二倍角的正弦公式和余弦公式和辅助角公式,结合正弦函数的值域,可得最值,解方程可得a,b,进而得到所求值.
解答 解:函数y=(acosx+bsinx)cosx
=a•$\frac{1+cos2x}{2}$+$\frac{bsin2x}{2}$
=$\frac{a}{2}$+$\frac{1}{2}$(acos2x+bsin2x)
=$\frac{a}{2}$+$\frac{1}{2}$$\sqrt{{a}^{2}+{b}^{2}}$sin(2x+θ)(θ为辅助角),
则f(x)的最大值为$\frac{a}{2}$+$\frac{1}{2}$$\sqrt{{a}^{2}+{b}^{2}}$,最小值为$\frac{a}{2}$-$\frac{1}{2}$$\sqrt{{a}^{2}+{b}^{2}}$,
由题意可得$\frac{a}{2}$+$\frac{1}{2}$$\sqrt{{a}^{2}+{b}^{2}}$=2,且$\frac{a}{2}$-$\frac{1}{2}$$\sqrt{{a}^{2}+{b}^{2}}$=-1,
解得a=1,b=±2$\sqrt{2}$,
则(ab)2=(±2$\sqrt{2}$)2=8.
故选:B.
点评 本题考查三角函数的化简和求值,考查辅助角公式和正弦函数的值域的运用,以及化简运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,+∞) | C. | (-∞,-$\frac{3}{2}$) | D. | (-$\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:解答题
在△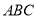 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是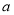 ,
,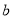 ,
,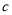 ,已知
,已知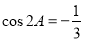 ,
, ,
,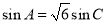 .
.
(1)求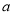 的值;
的值;
(2)若角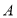 为锐角,求
为锐角,求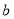 的值及△
的值及△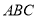 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$] | B. | (0,1] | C. | [-$\frac{1}{2}$,1] | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com