
【题目】已知函数![]() .
.
(1)设![]() 是
是![]() 的反函数.当
的反函数.当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)先由![]() ,得到
,得到![]() ,求出其反函数
,求出其反函数![]() ,解对应不等式,即可得出结果;
,解对应不等式,即可得出结果;
(2)先由![]() 得到
得到![]() ,分别讨论
,分别讨论![]() 和
和![]() 两种情况,即可得出结果;
两种情况,即可得出结果;
(3)根据复合函数单调性,得到![]() 在区间
在区间![]() 上单调递减,求出其最值,根据题意,得到
上单调递减,求出其最值,根据题意,得到![]() ,推出
,推出![]() 对任意的
对任意的![]() 恒成立,令
恒成立,令![]() ,求出
,求出![]() 的最大值,即可得出结果.
的最大值,即可得出结果.
(1)当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() ,
,
因为![]() 是
是![]() 的反函数,
的反函数,
所以![]() ,
,![]() ,
,
由![]() 得
得![]() ,所以:
,所以:![]() ,解得:
,解得:![]() ,
,
即不等式![]() 的解集为
的解集为![]() ;
;
(2)方程![]() 即
即![]() ,
,
所以![]() ,
,
①![]() ,则
,则![]() ,经过验证,满足关于
,经过验证,满足关于![]() 的方程
的方程![]() 的解集中恰好有一个元素;
的解集中恰好有一个元素;
②![]() 时,(i)若
时,(i)若![]() ,解得
,解得![]() ,代入
,代入![]() ,解得
,解得![]() ,经过验证,满足关于
,经过验证,满足关于![]() 的方程
的方程![]() 的解集中恰好有一个元素;
的解集中恰好有一个元素;
(ii)若![]() ,则
,则![]() ;
;
当![]() 时,由
时,由![]() 解得:
解得:![]() 或
或![]() ,即方程
,即方程![]() 的解要在
的解要在![]() 范围内,
范围内,
解方程![]() 得
得![]() ,因为
,因为![]() ,
,
所以为使关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,
的解集中恰好有一个元素,
只需![]() ,即
,即![]() ,显然不成立;
,显然不成立;
当![]() 时,由
时,由![]() 解得:
解得:![]() ,即方程
,即方程![]() 的解要在
的解要在![]() 范围内,
范围内,
解方程![]() 得
得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,且
,且![]() ,
,
因此只需![]() ,即
,即![]() ,
,
即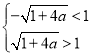 ,解得:
,解得:![]() ,与
,与![]() 矛盾,也不满足题意;
矛盾,也不满足题意;
综上,实数![]() 的值为
的值为![]() 或
或![]() ;
;
(3)由对数函数的单调性可得![]() 单调递增,根据幂函数单调性可得
单调递增,根据幂函数单调性可得![]() 在
在![]() 上单调递减,因为
上单调递减,因为![]() ,
,![]() ,
,
所以,根据复合函数单调性,可得![]() 在区间
在区间![]() 上单调递减,
上单调递减,
因此![]() ,
,![]() ,
,
又函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,
,
所以![]() ,
,
即![]() ,整理得
,整理得![]() ,即
,即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
令![]() ,
,![]() ,
,
任取![]() ,则
,则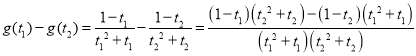
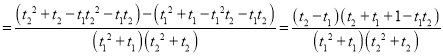 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
因此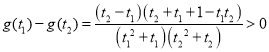 ,即
,即![]() ;
;
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
因此,只需![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() ,设
,设![]() 的内切圆分别与边
的内切圆分别与边![]() 相切于点
相切于点![]() ,已知
,已知![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与曲线E交于点
,与曲线E交于点![]() 轴,过
轴,过![]() 的另一直线与曲线
的另一直线与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在区间
,若在区间![]() 内有且只有一个实数
内有且只有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(1)判断函数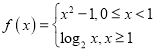 在区间
在区间![]() 内是否具有唯一零点,说明理由:
内是否具有唯一零点,说明理由:
(2)已知向量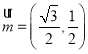 ,
,![]() ,
,![]() ,证明
,证明![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(3)若函数![]() 在区间
在区间![]() 内具有唯一零点,求实数
内具有唯一零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
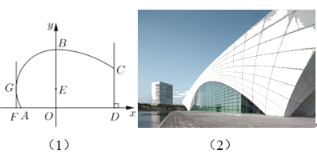
【题目】图(1)为东方体育中心,其设计方案侧面的外轮廓线如图(2)所示;曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() 且
且![]() 恰好等于圆
恰好等于圆![]() 的半径,
的半径,![]() 与圆相切且
与圆相切且![]() .
.
(1)若要求![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)当![]() 时,若要求
时,若要求![]() 不超过45米,求
不超过45米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线方程为![]() ,过其右焦点且斜率不为零的直线
,过其右焦点且斜率不为零的直线![]() 与双曲线交于A,B两点,直线
与双曲线交于A,B两点,直线![]() 的方程为
的方程为![]() ,A,B在直线
,A,B在直线![]() 上的射影分别为C,D.
上的射影分别为C,D.
(1)当![]() 垂直于x轴,
垂直于x轴,![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(2)![]() ,
,![]() 的斜率为正实数,A在第一象限,B在第四象限,试比较
的斜率为正实数,A在第一象限,B在第四象限,试比较![]() 与1的大小;
与1的大小;
(3)是否存在实数![]() ,使得对满足题意的任意
,使得对满足题意的任意![]() ,直线
,直线![]() 和直线
和直线![]() 的交点总在
的交点总在![]() 轴上,若存在,求出所有的
轴上,若存在,求出所有的![]() 值和此时直线
值和此时直线![]() 和
和![]() 交点的位置;若不存在,请说明理由.
交点的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com