练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知（1-x+x2）7=a0+a1x+a2x2+…+a14x14．求：
    （1）a0+a1+a2+…+a14．
    （2）a1+a3+a5+…+a13．

    分析 （1）在所给的等式中，令x=1，可得a0+a1+a2+…+a14=1  ①．
    （2）在所给的等式中，令x=-1，可得a0-a1+a2-a3+…+a14=37 ②，由①②求得要求的式子的值．

    解答 解：（1）在（1-x+x2）7=a0+a1x+a2x2+…+a14x14中，令x=1，
    可得a0+a1+a2+…+a14=1  ①．
    （2）（1-x+x2）7=a0+a1x+a2x2+…+a14x14中，令x=-1，
    可得a0-a1+a2-a3+…+a14=37 ②．
    由①-②可得2（a1+a3+a5+…+a13）=1-37，
    ∴a1+a3+a5+…+a13=$\frac{1{-3}^{7}}{2}$．

    点评 本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

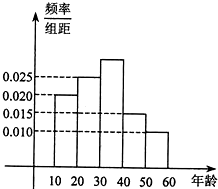    19．某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，远离毒品”的电视公益广告，期望让更多的市民知道毒品的危害性．禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段在[10，20），[20，30），[30，40），[40，50），[50，60）的市民进行问卷调查，由此得到样本频率分布直方图如图所示．
    （1）求随机抽取的市民中年龄段在[30，40）的人数；
    （2）从不小于40岁的人中按年龄段分层抽样的方法随机抽取5人，求[50，60）年龄段抽取的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数f（x）=2cos（x-$\frac{π}{3}$）的单调递增区间是（　　）
    A．[2kπ+$\frac{π}{3}$，2kπ+$\frac{4π}{3}$]（k∈Z）B．[2kπ-$\frac{π}{3}$，2kπ+$\frac{2π}{3}$]（k∈Z）
    C．[2kπ-$\frac{2π}{3}$，2kπ+$\frac{π}{3}$]（k∈Z）D．[2kπ-$\frac{2π}{3}$，2kπ+$\frac{4π}{3}$]（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

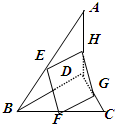    17．已知E、F、G、H分别为空间四边形ABCD的边AB、BC、CD、DA上的点，且EE=2，EH=1，四边形EFGH为平行四边形．
    （Ⅰ）求证：EH∥BD；
    （Ⅱ）连结AC，若AC⊥BD，求FH的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

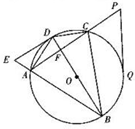    4．如图，过⊙O外一点P作一条割线与⊙O交于C、A两点，直线PQ切⊙O于点Q，BD为过CA中点F的⊙O的直径．
    （1）已知PC=4，PQ=6，求DF•BF的值；
    （2）过D作⊙O的切线交BA的延长线于点E，若CD=$\sqrt{10}$，BC=5，求AE的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若直线y=2x+m是曲线y=xlnx的切线，则实数m的值为（　　）
    A．eB．-eC．1D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合．曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=3，直线l的参数方程为$\left\{\begin{array}{l}x=-\sqrt{3}t\\ y=1+t\end{array}\right.$（t为参数，t∈R），
    （1）写出曲线C的直角坐标方程和直线l的普通方程；
    （2）试求曲线C上的点到直线l的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．假设200件产品中有3件次品，现在从中任取5件，至少有2件次品的抽法数有（　　）
    A．C${\;}_{3}^{2}$C${\;}_{198}^{3}$B．C${\;}_{3}^{2}$C${\;}_{197}^{3}$+C${\;}_{3}^{3}$C${\;}_{197}^{2}$
    C．C${\;}_{200}^{5}$-C${\;}_{197}^{4}$D．C${\;}_{200}^{5}$-C${\;}_{3}^{1}$C${\;}_{197}^{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．对于函数f（x），若存在x0∈R，使f（x0）=x0成立，则称x0为f（x）的不动点．如果函数f（x）=$\frac{{x}^{2}+a}{bx-c}$（b，c∈N*）有且仅有两个不动点0，2，且f（-2）＜-$\frac{1}{2}$．
    （1）试求函数f（x）的单调区间；
    （2）已知各项不为1的数列{an}满足${4S}_{n}•f（\frac{1}{{a}_{n}}）=1$，求证：-$\frac{1}{{a}_{n+1}}$＜ln$\frac{n+1}{n}$＜-$\frac{1}{{a}_{n}}$；
    （3）在（2）中，设bn=-$\frac{1}{{a}_{n}}$，Tn为数列{bn}的前n项和，求证：T2016-1＜ln2016＜T2015．

    查看答案和解析>>

    同步练习册答案