
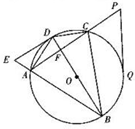
 如图,过⊙O外一点P作一条割线与⊙O交于C、A两点,直线PQ切⊙O于点Q,BD为过CA中点F的⊙O的直径.
如图,过⊙O外一点P作一条割线与⊙O交于C、A两点,直线PQ切⊙O于点Q,BD为过CA中点F的⊙O的直径.分析 (1)由切割线定理,可得PQ2=PC•PA,求出PA,计算出CA,可得AF,由相交弦定理,可得DF•BF;
(2)证明BD⊥DE,利用AD⊥AB,可得AD2=AB•AE,即可求AE的值.
解答 解:(1)由切割线定理,可得PQ2=PC•PA,
∴PA=$\frac{P{Q}^{2}}{PC}$=9,
∴CA=PA-PC=5,
∵F是CA的中点,
∴AF=FC=$\frac{5}{2}$.
由相交弦定理,可得DF•BF=AF•FC=$\frac{25}{4}$;
(2)∵BD是直径,F是AC的中点,
∴AD=CD=$\sqrt{10}$,AB-BC=5.
∵DE是切线,
∴BD⊥DE,
∵AD⊥AB,
∴AD2=AB•AE,
∴AE=$\frac{A{D}^{2}}{AB}$=2.
点评 相交弦定理、切割线定理注意用于与圆有关的比例线段的计算与证明,解决问题时要注意相似三角形与圆周角、弦切角、圆的切线、射影定理等相关知识的综合应用.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
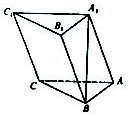 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
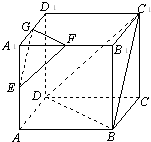 已知正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是AA1、A1B1、A1D1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是AA1、A1B1、A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A是锐角 | B. | B是锐角 | ||
| C. | C是锐角 | D. | △ABC是钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
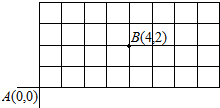 如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为$\frac{20}{243}$.
如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为$\frac{20}{243}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com