
| A. | A是锐角 | B. | B是锐角 | ||
| C. | C是锐角 | D. | △ABC是钝角三角形 |
分析 由a、b、c成等比,可得b2=ac,利用(a-c)2≥0,可得a2+c2≥2b2,利用余弦定理可求cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$≥$\frac{1}{2}$>0,结合范围B∈(0,π),即可得解B一定为锐角.
解答 解:∵a,b,c成等比,
∴b2=ac,
∵(a-c)2≥0,可得:a2+c2-2ac=a2+c2-2b2≥0,可得:a2+c2≥2b2,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$≥$\frac{2{b}^{2}-{b}^{2}}{2{b}^{2}}$=$\frac{1}{2}$>0,
∵B∈(0,π),
∴B一定为锐角.
故选:B.
点评 此题考查了余弦定理,等比数列的性质在解三角形中的应用,熟练掌握余弦定理是解本题的关键,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
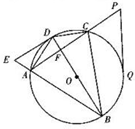 如图,过⊙O外一点P作一条割线与⊙O交于C、A两点,直线PQ切⊙O于点Q,BD为过CA中点F的⊙O的直径.
如图,过⊙O外一点P作一条割线与⊙O交于C、A两点,直线PQ切⊙O于点Q,BD为过CA中点F的⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三边都不等的三角形 | B. | 直角三角形 | ||
| C. | 等腰不等边三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<$\frac{2}{3}$ | B. | -1<m<$\frac{2}{3}$ | C. | $-\frac{1}{2}$<m<$\frac{2}{3}$ | D. | m>$-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com