
| A. | 三边都不等的三角形 | B. | 直角三角形 | ||
| C. | 等腰不等边三角形 | D. | 等边三角形 |
分析 由第一个条件可得角A的平分线和BC边垂直,△ABC为等腰三角形,且AB=AC.
再根据第二个条件利用两个向量的数量积的定义求得 cos∠A=$\frac{1}{2}$,可得∠A的值.
解答 解:∵非零向量$\overrightarrow{AB}$与$\overrightarrow{AC}$满足$({\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|}}+\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|}}})•\overrightarrow{BC}$=0,故角A的平分线和BC边垂直,
故△ABC为等腰三角形,且AB=AC.
∵2$\overrightarrow{AB}•\overrightarrow{AC}$=2AB•AC•cos∠A=|${\overrightarrow{AB}}$|•|${\overrightarrow{AC}}$|,
∴cos∠A=$\frac{1}{2}$,∴∠A=$\frac{π}{3}$,
则△ABC为等边三角形,
故选:D.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
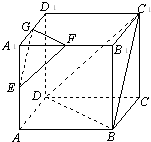 已知正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是AA1、A1B1、A1D1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是AA1、A1B1、A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A是锐角 | B. | B是锐角 | ||
| C. | C是锐角 | D. | △ABC是钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
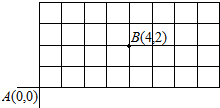 如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为$\frac{20}{243}$.
如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为$\frac{20}{243}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π-3}{2}$ | D. | $\frac{π}{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)g(a)=f(b)g(b) | B. | f(a)g(a)>f(b)g(b) | ||
| C. | f(a)g(a)<f(b)g(b) | D. | f(a)g(a)与f(b)g(b)大小关系不定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com