
分析 (1)①分别利用导数求出y=f(x)与y=h(x)在x=0的切线方程,根据两切线重合可求出a,b满足的条件;
②先求出函数F(x)的解析式,然后求出导函数F′(x),令F′(x)=0,讨论根的大小,从而求出函数的单调减区间;
(2)由集合{x|f(x)<g(x)}为空集,可知不等式f(x)≥g(x)对任意x∈R恒成立,即y=f(x)-g(x)≥0恒成立.
解答 解:(1)h(x)=ax2+bx+1
①∵f′(x)=ex,∴f′(0)=1,又f(0)=1,
∴y=f(x)在x=0处的切线方程为y=x+1…(2分)
又∵h′(x)=2ax+b,∴h′(0)=b,又h(0)=1,∴y=h(x)在x=0处的切线方程为y=bx+1,所以当a≠0,a∈R且b=1时,曲线y=f(x)与y=h(x)在x=0处总有相同的切线.…(4分)
(2)由a=1,$F(x)=\frac{{{x^2}+bx+1}}{e^x}$,∴$F′(x)=\frac{{-{x^2}+(2-b)x+b-1}}{e^x}$,
∴$F′(x)=\frac{{-{x^2}+(2-b)x+b-1}}{e^x}=-\frac{(x-1)(x-(1-b))}{e^x}$,…(6分)
由F′(x)=0,得x1=1,x2=1-b,∴当b>0时,函数y=F(x)的减区间为(-∞,1-b),(1,+∞);增区间为(1-b,1);
当b=0时,函数y=F(x)的减区间为(-∞,+∞);
当b<0时,函数y=F(x)的减区间为(-∞,1),(1-b,+∞),增区间为(1,1-b),…(9分)
(2)由集合{x|f(x)<g(x)}为空集,可知不等式f(x)≥g(x)对任意x∈R恒成立,即y=f(x)-g(x)≥0恒成立.…(10分)
当a≤0时,函数y=ex-ax-b在R上单调递增,y≥0不恒成立,所以a>0,此时y′=ex-a=0,解得x=lna,当x<lna时,y′<0,函数单调递减,当x>lna时,y′>0,函数单调递增,所以要使y=f(x)-g(x)≥0恒成立,
只需ymin=a-alna-b≥0,…(12分)
所以b≤a-alna,ab≤a2-a2lna,a>0,
令G(x)=x2-x2lnx,x>0,则G′(x)=2x-2xlnx-x=x(1-2lnx),
令G′(x)=0解得$x=\sqrt{e}$,当$x∈({0,\sqrt{e}})$时,G′(x)>0,函数G(x)单调递增,
当$x∈({\sqrt{e},+∞})$时,G′(x)<0,函数G(x)单调递减,
所以当$x=\sqrt{e}$时,函数G(x)=x2-x2lnx取得最大值$\frac{e}{2}$,所以$ab≤{a^2}-{a^2}lna≤\frac{e}{2}$,
所以ab的最大值为$\frac{e}{2}$.…(16分)
点评 本题考查了利用导数研究在曲线某点处的切线方程,利用导数研究函数的单调性,同时考查了不等式恒成立问题,解题过程中运用了构造函数的思想,是综合性较强的一道导数应用题.属于难题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [1,+∞) | C. | [2,+∞] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三边都不等的三角形 | B. | 直角三角形 | ||
| C. | 等腰不等边三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
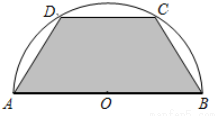 如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com