
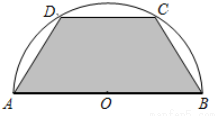
 如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.分析 如图所示,以直径AB所在的直线为x轴,线段AB中垂线为y轴,建立平面直角坐标系,过点C作CE⊥AB,
(I)由CD的长表示出OE的长,利用勾股定理表示出CE的长,利用梯形面积公式表示出y与x的函数关系式,并求出x的范围即可;
(II)把表示出y与x的关系式变形,令被开方数等于t,求出导函数t′,根据导函数的正负确定出函数的增减性,进而求出y的最大值即可.
解答 解:如图所示,以直径AB所在的直线为x轴,线段AB中垂线为y轴,建立平面直角坐标系,过点C作CE⊥AB,
(I)∵CD=2x,
∴OE=x(0<x<1),CE=$\sqrt{1-{x}^{2}}$,
∴y=$\frac{1}{2}$(|AB|+|CD|)•CE=$\frac{1}{2}$(2+2x)$\sqrt{1-{x}^{2}}$=(x+1)$\sqrt{1-{x}^{2}}$(0<x<1);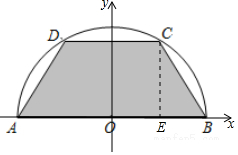
(II)y=$\sqrt{(x+1)^{2}(1-{x}^{2})}$=$\sqrt{-{x}^{4}-2{x}^{3}+2x+1}$,
令t=-x4-2x3+2x+1,
则t′=-4x3-6x2+2=-2(2x3+3x2-1)=-2(x+1)2(2x-1),
令t'=0,得到x=$\frac{1}{2}$或x=-1(舍),
∴当0<x<$\frac{1}{2}$时,t'>0,
∴函数在(0,$\frac{1}{2}$)上单调递增,
当$\frac{1}{2}$<x<1时,t'<0,
∴函数在($\frac{1}{2}$,1)上单调递减,
当x=$\frac{1}{2}$时,t有最大值$\frac{27}{16}$,ymax=$\frac{{3\sqrt{3}}}{4}$,
答:梯形部件y'=0面积的最大值为$\frac{{3\sqrt{3}}}{4}$平方米.
点评 此题考查了函数模型的选择与应用,熟练掌握导数在函数增减性中的应用是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{1}{4}$ | B. | ±$\frac{{\sqrt{2}}}{4}$ | C. | ±$\frac{1}{3}$ | D. | ±$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | -$\frac{\sqrt{10}}{10}$ | C. | ±$\frac{3\sqrt{10}}{10}$ | D. | ±$\frac{\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)g(a)=f(b)g(b) | B. | f(a)g(a)>f(b)g(b) | ||
| C. | f(a)g(a)<f(b)g(b) | D. | f(a)g(a)与f(b)g(b)大小关系不定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,2) | C. | (-∞,1)U(2,+∞) | D. | (-∞,1)U(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com