
分析 (1)求函数的导数,利用导数的几何意义以及切线方程建立方程关系即可求a,b值以及f(x)的单调区间;
(2)构造函数,利用导数研究函数的单调性和最值关系即可证明不等式.
解答 (1)解:f′(x)=ex+a,
由已知,f′(0)=-1,f(0)=-1,
故a=-2,b=-2,
f′(x)=ex-2,
当x∈(-∞,ln2)时,f′(x)<0,当x∈(ln2,+∞)时,f′(x)>0,
故f(x)在(-∞,ln2)单调递减,在(ln2,+∞)单调递增;…(6分)
(2)证明:设g(x)=f(x)-(x2-9)=ex-x2-2x+7,
g′(x)=ex-2x-2,
因为g′(0)=-1<0,g′(2)=e2-6>0,0<ln2<2,
所以g′(x)在[0,+∞)只有一个零点x0,且x0∈(0,2),${e}^{{x}_{0}}$=2x0+2,
当x∈[0,x0)时,g′(x)<0,
当x∈(x0,+∞)时,g′(x)>0,
即g(x)在[0,x0)调递减,在(x0,+∞)时,单调递增,
当x≥0时,g(x)≥g(x0)=${e}^{{x}_{0}}$-x02-2x0+7=9-x02>0,
即f(x)>x2-9,…(12分)
点评 本题主要考查导数的几何意义以及函数单调性的应用,综合考查导数的应用,运算量较大,综合性较强.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
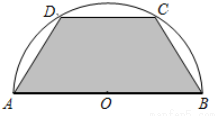 如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3+a7≥b2+b6 | B. | a3+a7≤b2+b6 | ||
| C. | a3+a7≠b2+b6 | D. | a3+a7与b2+b6 大小不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com