
分析 (1)利用函数f(x)=$\frac{{x}^{2}+a}{bx-c}$=x,可知:(1-b2)x2+cx+a=0,由韦达定理可知$\left\{\begin{array}{l}{2+0=-\frac{c}{1-b}}\\{2×0=\frac{a}{1-b}}\end{array}\right.$,由f(-2)=$\frac{-2}{1+c}$<-$\frac{1}{2}$,求得c的取值范围,即可求得c和b的值,即可求得函数的解析式,利用导数法求函数f(x)的单调区间;
(2)由题意可知:求得4Sn•$\frac{1}{{2a}_{n}(1-{a}_{n})}$=1,即可求得2Sn=an-${a}_{n}^{2}$,当n≥2时,2Sn-1=an-1-${a}_{n-1}^{2}$,两式相减得:(an+an-1)(an-an-1+1)=0,即可求得an=-an-1或an-an-1=-1,即可求得an=-n,构造辅助函数,求导,利用函数的单调性,即可求得$\frac{1}{x+1}$<ln$\frac{x+1}{x}$<$\frac{1}{x}$,x>0,继而求得-$\frac{1}{{a}_{n+1}}$<ln$\frac{n+1}{n}$<-$\frac{1}{{a}_{n}}$;
(3)bn=$\frac{1}{n}$,则${T_n}=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$,$\frac{1}{n+1}$<ln$\frac{n+1}{n}$<$\frac{1}{n}$中令n=1,2,3,…,2015,并将各式相加得T2016-1<ln2016<T2015.
解答 解:(1)设$\frac{{x}^{2}+a}{bx-c}$=x,则(1-b2)x2+cx+a=0,(b≠1),
∴0和2是方程的两个根,由韦达定理可知:$\left\{\begin{array}{l}{2+0=-\frac{c}{1-b}}\\{2×0=\frac{a}{1-b}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=0}\\{b=1+\frac{c}{a}}\end{array}\right.$,-----(1分)
∴f(x)=$\frac{{x}^{2}}{(1+\frac{c}{2})x-c}$,
由f(-2)=$\frac{-2}{1+c}$<-$\frac{1}{2}$,解得:-1<c<3,
又∵b,c∈N*,
∴c=2,b=2,
∴f(x)=$\frac{{x}^{2}}{2(x-1)}$(x≠1),-----(2分)
于是f′(x)=$\frac{2x×2(x-1)-{x}^{2}×2}{4(x-1)^{2}}$=$\frac{{x}^{2}-2x}{2(x-1)^{2}}$,
由f′(x)>0,解得x<0或x>2; 由f′(x)<0,解得0<x<1或1<x<2,
故函数f(x)的单调递增区间为(-∞,0)和(2,+∞),-----(3分)
单调减区间为(0,1)和(1,2)-----(4分)
(2)由已知可得${4S}_{n}•f(\frac{1}{{a}_{n}})=1$,4Sn•$\frac{1}{{2a}_{n}(1-{a}_{n})}$=1,
∴2Sn=an-${a}_{n}^{2}$,
当n≥2时,2Sn-1=an-1-${a}_{n-1}^{2}$,
两式相减得:(an+an-1)(an-an-1+1)=0,
∴an=-an-1或an-an-1=-1-----(5分)
当n=1时,2a1=a1-${a}_{1}^{2}$,解得:a1=-1,
若an=-an-1,则a2=1这与an≠1矛盾
∴an-an-1=-1,
∴an=-n-----(6分)
∴$\frac{1}{n+1}$<ln$\frac{n+1}{n}$<$\frac{1}{n}$,
为此,只要证明不等式$\frac{1}{x+1}$<ln$\frac{x+1}{x}$<$\frac{1}{x}$,x>0,
令1+$\frac{1}{x}$=t,x>0则t>1,x=$\frac{1}{t-1}$,
再令g(t)=t-1-lnt,g′(t)=1-$\frac{1}{t}$由t∈(1,+∞)知g′(t)>0,
∴当t∈(1,+∞)时,g(t)单调递增,
∴g(t)>g(1)=0,于是t-1>lnt,
即$\frac{1}{x}$>ln$\frac{x+1}{x}$,x>0 ①-----(8分)
令h(t)=lnt-1+$\frac{1}{t}$,h′(t)=$\frac{1}{t}$-$\frac{1}{{t}^{2}}$=$\frac{t-1}{{t}^{2}}$,
由t∈(1,+∞)知h′(t)>0,
∴当t∈(1,+∞)时,h(t)单调递增,
∴h(t)>h(1)=0,于是lnt>1-$\frac{1}{t}$,
即ln$\frac{x+1}{x}$>$\frac{1}{x+1}$,x>0 ②
由①、②可知$\frac{1}{x+1}$<ln$\frac{x+1}{x}$<$\frac{1}{x}$,x>0,
所以,$\frac{1}{n+1}$<ln$\frac{n+1}{n}$<$\frac{1}{n}$,即1-$\frac{1}{{a}_{n}}$<ln$\frac{n+1}{n}$<-$\frac{1}{{a}_{n}}$,
∴-$\frac{1}{{a}_{n+1}}$<ln$\frac{n+1}{n}$<-$\frac{1}{{a}_{n}}$;-----(9分)
(3)由(2)可知bn=$\frac{1}{n}$,则${T_n}=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$,
在$\frac{1}{n+1}$<ln$\frac{n+1}{n}$<$\frac{1}{n}$中令n=1,2,3,…,2015,
并将各式相加得:$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2016}<ln\frac{2}{1}+ln\frac{3}{2}+…+ln\frac{2016}{2015}<1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$,
即T2016-1<ln2016<T2015-----(12分)
点评 本题主要考查利用导数研究函数的单调性,数列与不等式的综合应用,函数的导数判断函数的单调性构造法的应用,分析法证明不等式的方法,属于难题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
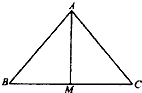 在△ABC中,点M是BC的中点,△AMC的三边长是连续的三个正整数,且tan∠C=$\frac{1}{tan∠BAM}$.
在△ABC中,点M是BC的中点,△AMC的三边长是连续的三个正整数,且tan∠C=$\frac{1}{tan∠BAM}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-3,3) | C. | (0,3) | D. | (1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com