
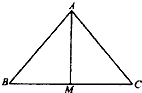
 在△ABC中,点M是BC的中点,△AMC的三边长是连续的三个正整数,且tan∠C=$\frac{1}{tan∠BAM}$.
在△ABC中,点M是BC的中点,△AMC的三边长是连续的三个正整数,且tan∠C=$\frac{1}{tan∠BAM}$.分析 (1)假设∠BAM=α,∠MAC=β,根据正弦定理可找到α,β与B,C的正弦之间的关系,进而再由诱导公式可确定α与β的关系.
(2)先设出3个连续的整数,再由勾股定理确定关系,根据余弦定理和二倍角公式可求出角BAC的余弦值.
解答 (本题满分为12分)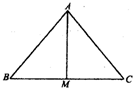 解:(1)设∠BAM=α,∠MAC=β,则由tanC=cotα,可得α+C=90°,
解:(1)设∠BAM=α,∠MAC=β,则由tanC=cotα,可得α+C=90°,
∴β+B=90°.…(1分)
△ABM中,由正弦定理得$\frac{BM}{sinα}=\frac{AM}{sinB}$,即$\frac{sinB}{sinα}=\frac{AM}{MB}$,同理得$\frac{sinC}{sinβ}=\frac{AM}{MC}$,…(3分)
∵MB=MC,
∴$\frac{sinB}{sinα}$=$\frac{sinC}{sinβ}$,
∴sinαsinC=sinβsinB,
∵α+C=90°,β+B=90°,
∴sinαcosα=sinβcosβ,…(5分)
即sin2α=sin2β,
∴α=β,或α+β=90°,
当α+β=900时,AM=$\frac{1}{2}$BC=MC,与△AMC的三边长是连续三个正整数矛盾,
∴α=β,∴∠B=∠C,
∴△ABC是等腰三角形.…(7分)
(2)在直角三角形AMC中,设两直角边分别为n,n-1,斜边为n+1,
由(n+1)2=n2+(n-1)2,得n=4,…(9分)
由余弦定理或二倍角公式得cos∠BAC=$\frac{7}{25}$,或cos∠BAC=-$\frac{7}{25}$.…(12分)
点评 本题主要考查正弦定理、余弦定理的应用.三角函数部分公式比较多,一定要强化记忆,属于中档题.


科目:高中数学 来源: 题型:解答题
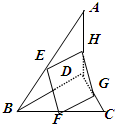 已知E、F、G、H分别为空间四边形ABCD的边AB、BC、CD、DA上的点,且EE=2,EH=1,四边形EFGH为平行四边形.
已知E、F、G、H分别为空间四边形ABCD的边AB、BC、CD、DA上的点,且EE=2,EH=1,四边形EFGH为平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{3}^{2}$C${\;}_{198}^{3}$ | B. | C${\;}_{3}^{2}$C${\;}_{197}^{3}$+C${\;}_{3}^{3}$C${\;}_{197}^{2}$ | ||
| C. | C${\;}_{200}^{5}$-C${\;}_{197}^{4}$ | D. | C${\;}_{200}^{5}$-C${\;}_{3}^{1}$C${\;}_{197}^{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$-1 | D. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com