
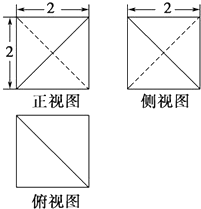
分析 借助常见的正方体模型解决.由三视图知,该几何体由正方体沿面AB1D1与面CB1D1截去两个角所得,其表面由两个等边三角形、四个直角三角形和一个正方形组成.计算得其表面积为12+4$\sqrt{3}$
解答 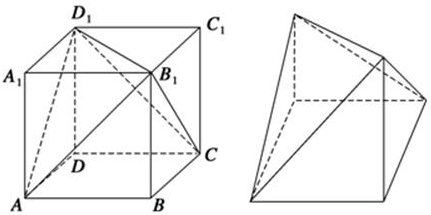 解:由三视图知,AB=BC=CD=DA=2,CE⊥平面ABCD,CE=2,
解:由三视图知,AB=BC=CD=DA=2,CE⊥平面ABCD,CE=2,
AE⊥平面ABCD,AE=2,
EF=2$\sqrt{2}$,BE=BF=DE=DF=2,
则△DEF,△BEF为正三角形,
则S△ABF=S△ADF=S△CDE=S△CBE=$\frac{1}{2}$×2×2=2,
S△BEF=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
S△DEF═$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,S正方形ABCD=2×2=4,
则该几何体的表面积S=4×2+2$\sqrt{3}$+2$\sqrt{3}$+4=12+4$\sqrt{3}$,
故答案为:12+4$\sqrt{3}$
点评 本题主要考查空间几何体的表面积,根据三视图确定对应几何体的边长关系是解决本题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+x+1 | B. | f(x)=x2-x-2 | C. | f(x)=x2-x+1 | D. | f(x)=x2+x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$+$\sqrt{2}$i | D. | $\sqrt{2}$-$\sqrt{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
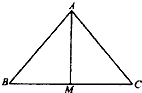 在△ABC中,点M是BC的中点,△AMC的三边长是连续的三个正整数,且tan∠C=$\frac{1}{tan∠BAM}$.
在△ABC中,点M是BC的中点,△AMC的三边长是连续的三个正整数,且tan∠C=$\frac{1}{tan∠BAM}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com