求值:4cos50°-tan40°=( )A．$\sqrt{2}$B．$\sqrt{3}$C．2$\sqrt{2}$-1D．$\frac{\sqrt{2}+\sqrt{3}}{2}$ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

2．求值：4cos50°-tan40°=（　　）

A．

$\sqrt{2}$

B．

$\sqrt{3}$

C．

2$\sqrt{2}$-1

D．

$\frac{\sqrt{2}+\sqrt{3}}{2}$

分析利用诱导公式化简，同角三角函数间的基本关系切化弦，再利用两角和与差的正弦、余弦函数公式化简，整理可得到结果．

解答解：4cos50°-tan40°=4sin40°-tan40°
=$\frac{4sin40°cos40°-sin40°}{cos40°}$=$\frac{2sin80°-sin（30°+10°）}{cos40°}$
=$\frac{2cos10°-\frac{1}{2}cos10°-\frac{\sqrt{3}}{2}sin10°}{cos40°}$=$\sqrt{3}$•$\frac{\frac{\sqrt{3}}{2}cos10°-\frac{1}{2}sin10°}{cos40°}$
=$\sqrt{3}$•$\frac{cos（30°+10°）}{cos40°}$=$\sqrt{3}$，
故选：B．

点评本题考查了两角和与差的正弦、余弦函数公式，同角三角函数间的基本关系，以及诱导公式的作用，熟练掌握公式是解本题的关键，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

12．定义在[-3，3]的偶函数f（x）且满足f（x+1）=f（x-1），当x∈[0，1]时，f（x）=cosx，则y=f（x）与y=lgx的图象的交点个数为0．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．

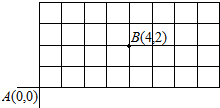如图，在网格状小地图中，一机器人从A（0，0）点出发，每秒向上或向右行走1格到相应顶点，已知向上的概率是$\frac{2}{3}$，向右的概率是$\frac{1}{3}$，问6秒后到达B（4，2）点的概率为$\frac{20}{243}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．已知a、b∈R，集合A={a，a+b，1}，B={b，$\frac{b}{a}$，0}，且A⊆B，B⊆A，求a-b的值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

17．已知实数m∈[0，1]，n∈[0，2]，则关于x的一元二次方程4x²+4mx-n²+2n=0有实数根的概率是（　　）

A．

1-$\frac{π}{4}$

B．

$\frac{π}{4}$

C．

$\frac{π-3}{2}$

D．

$\frac{π}{2}$-1

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．

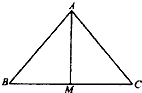在△ABC中，点M是BC的中点，△AMC的三边长是连续的三个正整数，且tan∠C=$\frac{1}{tan∠BAM}$．
（1）判断△ABC的形状；
（2）求∠BAC的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．已知椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点与短轴的一个端点是直角三角形的3个顶点，直线l：y=-x+3与椭圆E有且只有一个公共点T．设O是坐标原点，直线l'平行于OT，与椭圆E交于不同的两点A、B，且与直线l交于点P．若存在常数λ，使得|PT|²=λ|PA|•|PB|，则λ=$\frac{4}{5}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．在△ABC中，A=60°，a=$\sqrt{7}$，三角形面积为$\frac{3\sqrt{3}}{2}$，求b，c．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．定义在R上的奇函数f（x）满足f（x-4）=-f（x），且在（0，2]上单调递增，则（　　）

A．

f（-25）＜f（19）＜f（40）

B．

f （40）＜f（19）＜f（-25）

C．

f（19）＜f（40）＜f（-25）