
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图2).
(如图2).![]() 为
为![]() 中点
中点
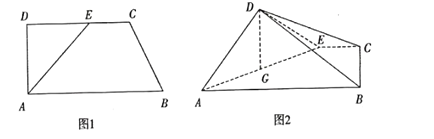
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
【答案】(1)证明见解析(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)证明DG⊥AE,再根据面面垂直的性质得出DG⊥平面ABCE即可证明
(2)分别计算DG和梯形ABCE的面积,即可得出棱锥的体积;
(3)过点C作CF∥AE交AB于点F,过点F作FP∥AD交DB于点P,连接PC,可证平面PCF∥平面ADE,故CP∥平面ADE,根据PF∥AD计算![]() 的值.
的值.
(1)证明:因为![]() 为
为![]() 中点,
中点,![]() ,所以
,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,故
,故![]()
(2)在直角三角形![]() 中,易求
中,易求![]() ,则
,则![]()
所以四棱锥![]() 的体积为
的体积为![]()
(3)存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() =3:4
=3:4
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
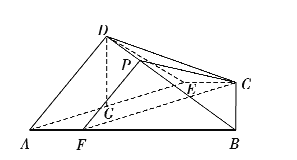
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() .
.
又因为![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() .又因为
.又因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,由
,由![]() ,则
,则![]() =3:4
=3:4


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】![]() 是亚太区域国家与地区加强多边经济联系、交流与合作的重要组织,其宗旨和目标是“相互依存、共同利益,坚持开放性多边贸易体制和减少区域间贸易壁垒.”2017年
是亚太区域国家与地区加强多边经济联系、交流与合作的重要组织,其宗旨和目标是“相互依存、共同利益,坚持开放性多边贸易体制和减少区域间贸易壁垒.”2017年![]() 会议于11月10日至11日在越南岘港举行.某研究机构为了了解各年龄层对
会议于11月10日至11日在越南岘港举行.某研究机构为了了解各年龄层对![]() 会议的关注程度,随机选取了100名年龄在
会议的关注程度,随机选取了100名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
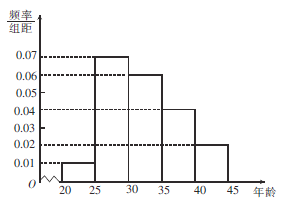
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人参与![]() 会议的宣传活动,求参与宣传活动的市民中至少有一人的年龄在
会议的宣传活动,求参与宣传活动的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三个内角
三个内角![]() 所对的边分别是
所对的边分别是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圆半径为2,求
的外接圆半径为2,求![]() 周长的最大值.
周长的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由正弦定理将边角关系化为边的关系![]() ,再根据余弦定理求角
,再根据余弦定理求角![]() ,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
试题解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因为![]() ,则
,则![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周长![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴当![]() 即
即![]() 时
时![]()
∴当![]() 时,
时, ![]() 周长的最大值为
周长的最大值为![]() .
.
【题型】解答题
【结束】
18
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中:  ,
, ![]() ,
, ![]()

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学假期社会实践活动选定的课题是“节约用水研究”.为此他购买了电子节水阀,并记录了家庭未使用电子节水阀20天的日用水量数据(单位:![]() )和使用了电子节水阀20天的日用水量数据,并利用所学的《统计学》知识得到了未使用电子节水阀20天的日平均用水量为0.48
)和使用了电子节水阀20天的日用水量数据,并利用所学的《统计学》知识得到了未使用电子节水阀20天的日平均用水量为0.48![]() ,使用了电子节水阀20天的日用水量数据的频率分布直方图如下图:
,使用了电子节水阀20天的日用水量数据的频率分布直方图如下图:
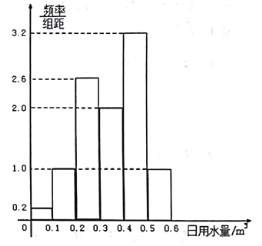
(1)试估计该家庭使用电子节水阀后,日用水量小于0.35![]() 的概率;
的概率;
(2)估计该家庭使用电子节水阀后,一年能节省多少![]() 水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了选拔学生参加“全国高中数学联赛”,先在本校进行初赛(满分150分),随机抽取100名学生的成绩作为样本,并根据他们的初赛成绩得到如图所示的频率分布直方图.

(1)求频率分布直方图中a的值;
(2)根据频率分布直方图,估计这次初赛成绩的平均数、中位数、众数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地统计局调查了10000名居民的月收入,并根据所得数据绘制了样本的频率分布直方图如图所示。

(1)求居民月收入在[3000,3500)内的频率;
(2)根据频率分布直方图求出样本数据的中位数;
(3)为了分析居民的月收入与年龄、职业等方面的关系,必须按月收入再从这10000中用分层抽样的方法抽出100人做进一步分析,则应从月收入在[2500,3000)内的居民中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县大润发超市为了惠顾新老顾客,决定在2019年元旦来临之际举行“庆元旦,迎新年”的抽奖派送礼品活动.为设计一套趣味性抽奖送礼品的活动方案,该超市面向该县某高中学生征集活动方案.该中学某班数学兴趣小组提供的方案获得了征用.方案如下:将一个![]() 的正方体各面均涂上红色,再把它分割成64个相同的小正方体.经过搅拌后,从中任取两个小正方体,记它们的着色面数之和为
的正方体各面均涂上红色,再把它分割成64个相同的小正方体.经过搅拌后,从中任取两个小正方体,记它们的着色面数之和为![]() ,记抽奖中奖的礼金为
,记抽奖中奖的礼金为![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)凡是元旦当天在超市购买物品的顾客,均可参加抽奖.记抽取的两个小正方体着色面数之和为6,设为一等奖,获得价值50元礼品;记抽取的两个小正方体着色面数之和为5,设为二等奖,获得价值30元礼品;记抽取的两个小正方体着色面数之和为4,设为三等奖,获得价值10元礼品,其他情况不获奖.求某顾客抽奖一次获得的礼金的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com